Last Updated on January 14, 2026 by Maged kamel
What is Newton-divided difference interpolation?
Newton has developed a new method for interpolating functions. In this post, we will discuss Newton-divided-difference interpolation.
A new form of Quadratic expression was adopted. For a Quadratic function where n=2, we need n+1 points, three points. Our n+1=3 points, namely (xo, x1, x2), and their y coordinates are (yo, y1, y2).
The quadratic function will be written as Q(x) = b0+b1(x-x0) +b2(x-x0) (x-x1). It can be further expanded as Q(x) = bo+b1x- b1*xo +b2(x^2-x*x1-x0*x+x0 *x1). Recalling our polynomial expressed as P2(x)= ao+a1*x+a2*x^2.
Since both functions are the same, we will set them equal. For the item x, we have a1*x = b1*x + b2*x1*x + b2*x0*x. a1= b1 -b2*x1 -b2*x0.

Similarly, for the item of x^2, we have a2*x^2=b2*x^2. Then, for the value of the term a2, it will be a2= b2
For the constant item, we have a0= b0-b1*x0+b2*x0*x1. To get the values of b0, b1, and b2 in terms of the given three Points. Use the first point(x0,y0) to get the value of b0. We can rewrite the Q(x0) as: x=x0,y=y0.
Q(x) = b0+b1(x-x0) +b2(x-x0) (x-x1). Q(x0) =y0= b0+b1(x0-x0) +b2(x0-x0) (x0-x1). b0=y0.
Back to our equation of Q(x), Q(x) = y0+b1(x-x0) +b2(x-x0) (x-x1). For the second point(x1,y1), we can rewrite the Q(x1) as: x=x1,y=y1. From the equation Q(x) = y0+b1(x-x0) +b2(x-x0) (x-x1).

The expression of the first divided difference.
Q(x1) =y1= y0+b1(x1-x0) +b2(x1-x0) (x1-x1). y1= y0+b1(x1-x0)+0 then b1=(y1-y0)/(x1-x0). This is the first divided difference written as f (x0, x1).

The following slide shows a detailed set of steps to derive an expression for b1.
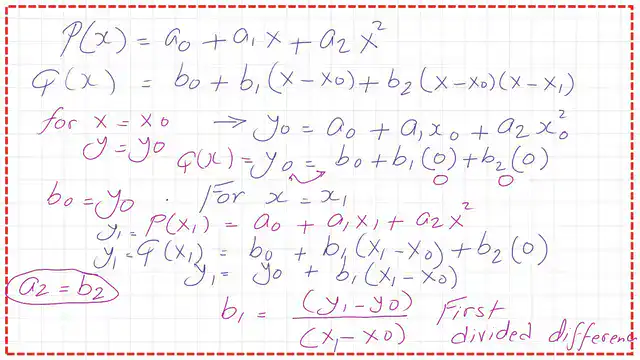
Back to our equation of Q(x). Q(x) = y0+b1(x-x0) +b2(x-x0) (x-x1). Rewrite as: Q(x) = y0+((y1-y0)/(x1-x0))* (x-x0) +b2(x-x0) (x-x1). For the third point (x2,y2), we can rewrite the Q(x2) as: x=x2,y=y2.
From the equation Q(x) = y0+((y1-y0)/(x1-x0))* (x-x0) +b2(x-x0) (x-x1).
We plug in the values x = x2 and y = y2 into the Q(x) equation and substitute the value of b1 we obtained earlier.
The following steps on the next slide picture illustrate the procedure for obtaining the value of b2.

Newton-divided difference or second-divided difference.
For the second divided-difference, which is written as f, bracket x0,x1,x2, then bracket.

This is the final expression for the quadratic polynomial using Newton-divided difference interpolation.
The polynomial is shown in the case of the first order.

The first divided difference is shown in the next slide. A line represents the first divided difference.
The slope alpha is the divided difference between (x0 and x1) points, which is equal to the rise over the run shown in the case of the first order.

For the Higher-order n value, an expression can be developed and made into a table.
We can make a table for the second divided difference. The next slide image shows the arrangement. The source is from Amos Gilat’s Numerical Methods for Engineers. The clouded area is for a Quadratic polynomial.
The term b0 starts with the first point (x0, y0); if the points start at x1, then the first term is b1.
In the following slide, the terms a1, a2, a3, …, a5 are used.

The main advantage of Newton’s divided difference interpolation is that we do not need to substitute in it to make a solution for the n equations. In our case, n=2 is for a quadratic function.
The PDF data for this post can be viewed or downloaded from the following document.
The next post will solve two practice problems on Newton-Divided difference polynomials.
This is a Wiki link for Numerical analysis.
This is a link to Holistic Numerical Methods-Newton Divided Differences.