Last Updated on May 20, 2024 by Maged kamel

Solved problems for Newton-divided differences.

We have discussed the Newton-divided difference interpolation in a previous post. In this post, we have two solved problems as an application to Newton-divided differences.

The first solved problem.

Three points where x and y values are given are required to get the expression for the polynomial based on Newton-divided differences and the value of a new point with x=2.70.

The next equation will obtain the polynomial, but we need to estimate the values of b₀,b₁, and b₂. We could start the first point and call it (?x1,y1), but in these two solved problems, I consider the first point coordinates as (X0, y0).

We know that b₀=y₀, from the given table, the first point y value or y0=3.
To get the b1, we must estimate the first divided difference between x₀,y_0, and(x₁,y₁).

The Graph curve based on the given points is shown in the next slide image. We have three points, meaning we have three’ coefficients: b0, b1, and b2. the polynomial P(x) =b0+b0*(x-x0)+b2*(x-x0)*(x-x1). Such an expression will give p(x=x0)=b0, while P(x=x1)=b0+b1*(x1-x0)+b2*(x1-x0)*(x1-x1)=b0+b1*(x1-x0)+0.

The first coefficient, b0, is equal to the y coordinate of the first point, so b0=y0.

How do we estimate the b0, b1, and b2 values?

The shown equation gives the second divided difference in the next slide image.

The first divided difference between points (x₁, y₁) and ( x₀,y₀) is estimated as the difference between (y₁ and y₀)/the difference between x₁ and x₀.

After estimating the first two differences, the value of these differences will be divided by the difference between(x₂-x₀) to get the second divided difference. the coefficient b0=3, while b1=(y1-y0)/(x1-x0)=(5-3)/(2-1), f[x1,x2)=(y2-y1)/(x2-x1)=(8-5)/(3-2)=3, b2=f[x1,x2)-f[x1,x2)/(x3-x0)=1/2.

Once we have obtained the three values of b₀,b₁, and b2, we can write the polynomial, as the next slide image shows.

The final expression for the polynomial using Newton-divided differences.

The next slide image shows the final expression for the polynomial using Newton-divided differences.

The last requirement is to estimate the y value for a new point of a given x value =2.70. Before we can substitute the value of x=2.7 in the polynomial expression, it is preferred to check the y values of the given three points via the table using the values obtained using the polynomial expression for (x₀,x₁,x₂).

From the shown calculations, we can substitute the value of x=2.70 and get the P(2.70), which is equal to 6.995.

The second solved problem.

Four points where x and y values are given require getting the expression for the polynomial based on Newton-divided differences. Since we have four points, we have to determine the values of four b’s: b₀,b₁,b₂, and b₃.

The equation will now be expanded to account for the four values of b’s.

How do we estimate the value of b₁?

The value of b₀ is the same value of y₀ for the first point, which equals 1. For the value of b₁, it will be estimated as the first divided difference between points (x₀,y₀) and (x₁,y₁).

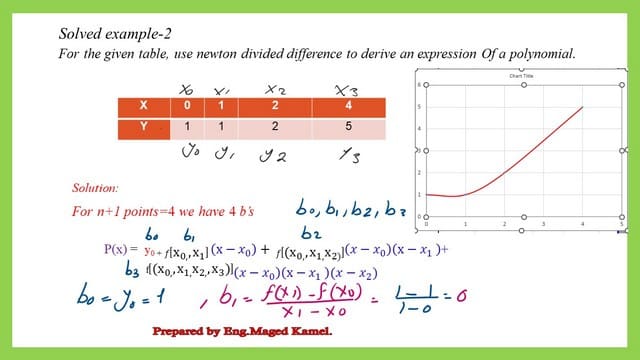
How do we estimate the value of b₂?

The b₂ values can be estimated in two stages. The first stage is to get the first divided difference between points (x₂,y₂) and ( x₁,y₁).

The second stage is to get the first divided difference between points (x₀,y₀) and ( x₁,y₁). The estimated differences will be divided by (x₂-x₀).

This table is used to get the differences for the 4 given points in the case of a cubic polynomial, which is a polynomial of degree 3. The equations of b₀,b₁,b₂, and b₃ are shown in the slide image.

How do we estimate the value of b₃?

The given calculation for the value of b3 is given in the next slide image for more details.

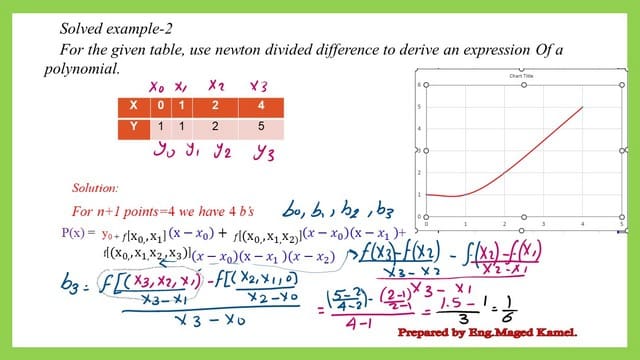
The final value of b₃ is shown to be=-1/12.

A table was used to get the Newton-divided differences.

It is much easier to estimate the divided differences and get the different values of b₀,b₁,b₂, and b₃ by using the table.

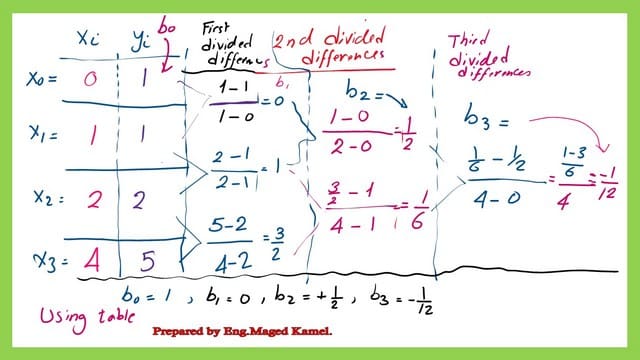
Once we have obtained the three values of b₀,b₁,b₂, and b₃.

The final expression for the polynomial using Newton-divided differences.

The expression of the cubic function is shown. The given table compares all the y values of the given four points, estimated by plugging the polynomial expression, and finds that they match.

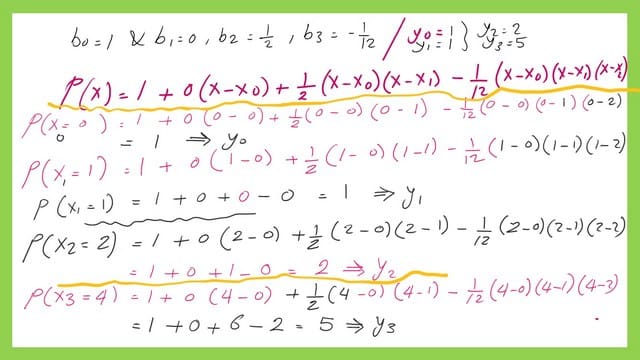
We can find the polynomial, as we can see from the next slide image. It is preferred to check the y values of the given four points via the table using the values obtained by using the polynomial expression for (x₀,x₁,x₂,x₃).

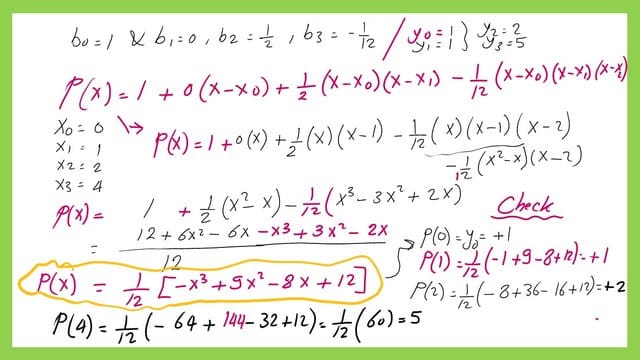
This is a link to Holistic Numerical Methods-Newton divided Differences.

This links to the previous post: What is Newton-divided difference interpolation?