7-A Solved problem 9-5 LU decomposition.

Last Updated on December 17, 2025 by Maged kamel

A solved problem 9-5 LU decomposition.

This solved problem 9.5 from Prof. Chapra’s reference book Numerical Methods for Engineers.

It is required to solve three simultaneous equations by the Lu decomposition for a 3×3 matrix, we are going to solve this problem by using LU factorization(decomposition).

Matrix A is the matrix for the (3×3) variables. The first row is (3 -0.10 -0.20), which will be reserved for (U11, u12, u13) elements for the Upper matrix U1.

Step-1-Derive the expression for U1 and L1 matrices for the solved problem 9-5 LU decomposition.

For the upper matrix U1, we have the first row set as(3 -0.10 -0.20), being an upper matrix (U21 and U21 should be =0, This is done by using a factor (-a21/a11) and factor (-a32/a11).
The first factor is to be multiplied by R1 and added to R2. The second factor will be multiplied by R1 and added to R3.

As we can see from the next slide image: (-a21/a11)=-(0.10/3). multiply by R1+R2, then for U21=-(0.10/3)*3+0.10=0. While for u22=(-010/3)*-0.10+7=7.003. for u23=(-010/3)*-0.20+(-0.30)=-0.2933.

For the elements of the lower matrix L1, we have a diagonal of +1, and the upper elements l11, l12, and l13 are 0. For L21=-(-a21/a11)=+0.033, l31=-1(-a33/a11)=-1(-0.30/3)=+0.1. The unknown element is l23 that element will be estimated i the next step.

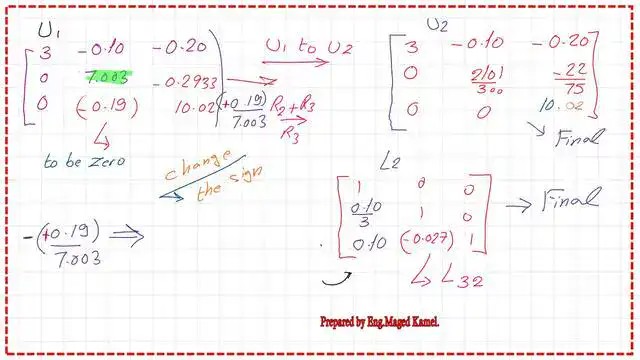
Step-2-Derive the expression for U and L matrices for the Solved problem 9-5 LU decomposition.

For u32 to be zero, multiply by (+0.19/7.003), using 7.003 as a pivot, then multiply by R2 and add to R33, u32 (0.19/7.003)*7.003+(-0.19)=0. The reversed sign for this factor (-0.19/7.003) yields L32 = -0.027.

The element of L2 will be the final elements for L matrix as(1 0 0, 0 1 0, 0.10 -0.027 1). The elements of the U2 matrix will be the final elements of the U matrix: (3, -0.10, -0.20, 0, 0, 0, 0, 1, 0, 0.10, -0.027, 1).

Step-3-Derive the expression for the inverse matrices L-1 and U-1 for the Solved problem 9-5 LU decomposition.

Step-4-Derive the value for the C matrix for the Solved problem 9-5 LU decomposition.

The matrix A can be represented as the product L*U, where L is the lower matrix, and U is the upper matrix. We need to get the inverse matrices L-1 and u-1.

We can determine the elements of these two inverted matrices using an Excel sheet, as shown in the next slide.

Now for the expression of AX=B, since A=LU, So AX=LUX=B. Consider UX=C, while L* C=B, we can get the elements of matrix C by multiplying both sides by the inverted matrix L-1.

L-1*B ( 1 0 0, -0.03333 1 0, -0.100904 0.027129 1) by (7.85 -19.3 71.40). This will create a matrix C (3×1) matrix which can be presented as ( 7.85 -19.5617 70.0842).

Step-5-get the values for x1, x2, x3 for the X-matrix for the Solved problem 9-5 LU decomposition.

After we obtain the values for the C matrix, we will consider the expression U*X=C and multiply both sides by U-1 to get the value of the X matrix, which is a (3×1) matrix. The inverse matrix U-1 is (0.3333 0.00475 0.006793,0 0.142789 0.00418, 0 0 0.0998). This matrix is to be multiplied by the C matrix. The final value of X – the matrix can be estimated as a (3×1) matrix, (2.9996 -2.5002 6.99444).

This solution is very close to Prof. Chapra’s, as shown in the last slide image.

This is the PDF file for the content of this post.

The following post: Step-by-step Introduction to Crout’s LU decomposition for a 2×2 matrix.

This is the Omni calculator for estimating various linear algebra items – LU Decomposition Calculator.

This is a link to another –Calculator for matrices.