Last Updated on June 20, 2025 by Maged kamel
This post is about the Universal set and its subsets. Solved problems are introduced to clarify the idea.
Introduction to the Universal set and subsets of sets.
What is the subset?
I quote, if every element of A is also an element of B. if whenever x ∈A, as x is a part of A, then x ∈ B, then x is an element of B.
The graph shows A as a small circle inside the big circle, which is B. If all the elements in x, located at A also exist in B.
It means that A is a subset of B; this is logic. The shapes used are called Venn diagrams, a diagram style that shows the logical relation between sets. The symbol used is A⊆B. A is a subset of B. Set A is included in set B.
Suppose A intersects with B. Then, A is partially part of B but not fully. Then A is not a subset of B. To explain that, another symbol is used, which is A⊄B. Set A is not a subset of set B.

A solved problem-5.
Solved problem # 5, if set A = {1,2,3,4,5,6}, while Set B {2,4,5} and set C = {1,2,3,4,5}, it is required to show the Venn diagram.
We can draw each set as circles. Set A includes numbers from A to 6; the second circle is for B, which contains 2,4,5. At the same time, C is another circle that provides for 1,2,3,4,5.
The biggest circle A is drawn first the numbers are from 1 to 6. We can select b part that includes 2,4,5 and make other shapes. We can choose the C part that provides for 1, 2, 3, 4, and 5 as a new shape.
The only remaining part for A is number 6. A is the biggest shape, B is the smallest figure, and C is the middle shape. if we need to express ourselves, we start with the smallest to the biggest.
Set B is a subset of A, and C is also a subset of A. Set B is a subset of C. If we start from the biggest 5 shapes toward the smallest shape A, the biggest shape is not a subset of B, also A is not a subset of C. C which is bigger than B is not a subset of B.
A solved problem-6.
A solved problem number #6, if set A={1,2,3,4}, if set B={1,4}, while set C={1}. Describe which is the subset. Check the biggest, A, followed by B, then C is the smallest. Also, check the smallest to the biggest.
B is a subset of A for the smallest to biggest relation, since B is smaller than A. B contains 1,4, which are included in A. C is also a subset of A since element 1 is included in set A. C is a subset of B since element 1 is included in set B. But A is not a subset of B, A is >B. A is not a subset of C; A is >C.
Solved Problems-7-8.
Let us check the solved problem #7, set M ={a,b}, how many subsets are there? What are the different alternatives? We have phi x, Ø. M has 4 substets,A={a}, B={b}, {a,b} ,Ø.
Solved problem #8, how many subsets for M. ={a,b,c}?
The answer is that the following subsets are A {a}. B={b}, C={c}, later start to use the mix {a,b,c}, null, so far we have selected 5 choices. Add the alternatives {a,c},{a,b},{b,c}. We have a total of 8 subsets, all are {a},{b},{c},{a},Ø = {},{a,b,c},{a,b},{a,c}.
Universal set.
The new item, capital U, is drawn as a rectangle for any particular problem and is a set that contains all the possible elements of the problem.
A solved problem-9.
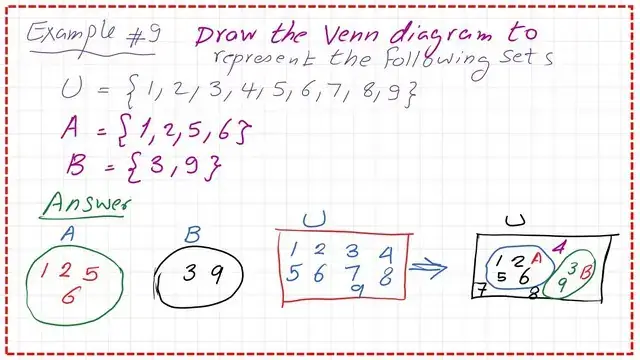
Let us have a Solved problem-9, if U={1,2,3,4,5,6,7,8,9}, while A={1,2,5,6}. While B={5,6}.
Draw a Venn diagram to represent these sets. If we draw each set separately. This is the circle that represents A={1,2,5,6}
B={3,9}. This is the U {1,2,3,4,5,6,7,8,9}. For the Venn diagram, draw the big box to represent U and draw shapes for A and B, which include each element. For A, take {1,2,5,6} and draw a shape, then select B ={3,9} and draw a shape.
How many total elements do we have? We have nine elements. We have already used four elements for A and two for B, so the remaining three elements are expected to be used.
Checking the remaining elements, we will find that these elements are 4,7,8.
For an external link, math is fun for a Venn diagram.
The following post, Complement of a set, Cumulative, associative, Distributive of sets.




