11-Moment of inertia Iy-Case-2 for a right-angle triangle.

Last Updated on December 31, 2025 by Maged kamel

Moment of inertia Iy-Case-2 for a right-angle triangle.

Case of Moment of inertia Iy-case-2-for y-axis at the left side.

There are two conditions for the y-axis: the first is when the y-axis passes by the intersection point between the base and the hypotenuse, or the left corner.
1-For Iy estimation,  for case -2, a vertical strip will be used, the strip width is dx, and its height is y.            
  2- Since the strip height starts from the base and intersects with line  AC, the y value is the same as the line AC equation, that is, y=h*x/b, for the x value it will be=b*y/h.  
3- The moment of Inertia due to that strip about the Y-axis is equal to A*(x^2).

4- Integrate from x=0 to x=b. Iy=(h*b^3)/4 is the final solution. This is a right-angle triangle’s Inertia Iy-case-2.

   
The radius of gyration Ky for a right angle. 

   5- From the expression that Ky=sqrt(Iy/A), we can get the radius of gyration about the y-axis, since A=(1/2)b*h. The value of the moment of inertia, Iy=h*b^3/4. Then Ky=sqrt(h*b^3/4)/(1/2*b*h)= h/sqrt(2).                   

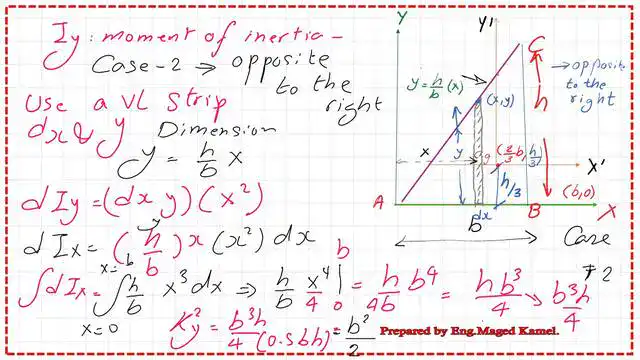
Moment of inertia Iy-Case-2 for right-angle, case of the Y axis is at the right side.

Let’s say we wish to move the Y-axis such that it, for instance, coincides with the triangle’s other side.
The y-axis coincides with the other side of the triangle, while the x-axis points left.
Once more, we’ll employ a vertical strip with height = y and width = dx.

1-For the estimation of Iy -case -2, a vertical strip will be used, the strip width is dx, and its height is y.       
2- Since the strip height starts from the base and intersects with line  AC, the y value is the same as the line AC equation y=(h/b)*(b-x).
3-Moment of inertia due to that strip=dA*(x^2).
4- We will integrate from x=0 to x=b; the details of the integration are shown in the next slide. The final answer is Iy=h*b^3/12.    
When comparing this value with the previous Iy value, we find that Iy decreases, and the radius of gyration Ky for right-angle case 2 increases when the y-axis is on the right side.   

5- From the expression that Ky=sqrt(Iy/A), we can get the radius of gyration about the y-axis, since A=(1/2)b*h.
Iy=h*b^3/12. Then Ky=sqrt(h*b^3/12)/(1/2*b*h)= h/sqrt(6).      

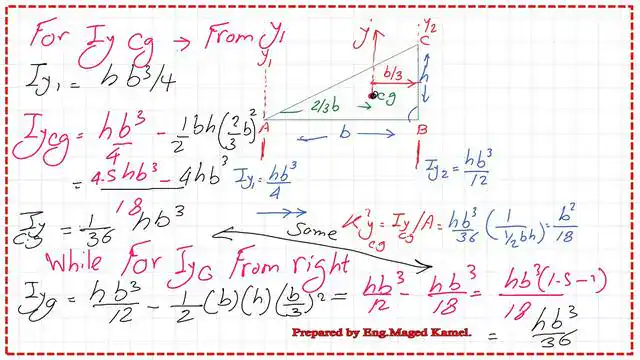
Inertia Iy at the CG for a right-angle triangle.

1-For Iyg estimation, we will deduct the product of A*x_bar^2, from the Iy-inertia-case-2-Iy value which is =h*b^3/4.
 2-We get the value of Iyg=h*b^3/36, which was derived from the case where the y-axis is located on the left side, I call it Y1, as shown in the slide.

3- The moment of inertia about the CG-Iyg value for the second case, where the y-axis is located on the right side, is the same value after subtracting Ax bar^2 from Iy value =hb^3/12 for the expression of Iy.

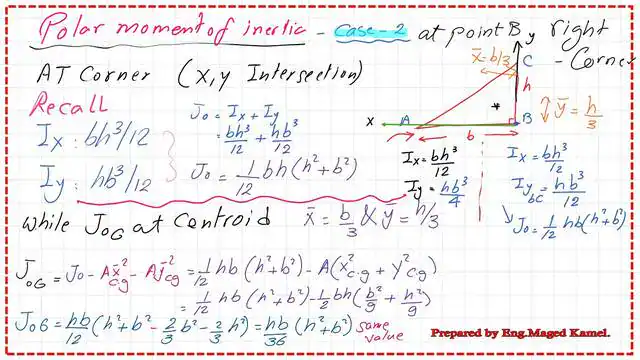
Polar Moment of inertia Jo for a right-angle for the y-axis at the left side.

The polar moment of inertia Jo for the right-angle case 2 for the y-axis at the left side can be estimated by adding the sum of Ix and Iy. We have Ix = bh^3/12, while Iy = hb^3/4 when the y-axis is at the left. That position will be called Y1.
Jo=(bh^3/12)+(hb^3/4).

The final value for J0G, which is the polar moment of inertia at the Cg can be written as The steps to get the polar moment of inertia at the CG.

The polar moment of inertia Jo for case 2, right-angle, about the y-axis on the right.

The polar moment of inertia, Jo, can be estimated as the sum of Ix and Iy. We have Ix value =bh^3/12, while Iy=hb^3/12 when the y-axis is located at the right, that position will be called Y. Jo=(bh^3/12)+(hb^3/12).

To get the value of the polar moment of inertia for the right-angle triangle. at the CG, deduct Ax^2 plus Ay^2cg from Jo, we have Xcg equals b/3, while ycg=h/3. Jocg=1/12*h*b*(h^2+b^2)-1/2*(bh)*(x^2cg+ycg^2). the final value of jcg=1/36*(h*b)(b^2+h^). The result matches the previously estimated Jcg value when the x and y axes are at the left corner.

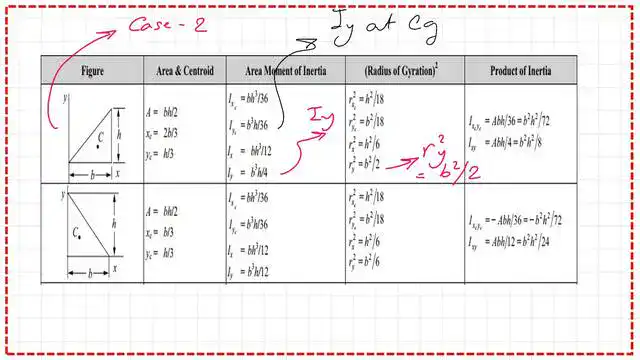
This is the table for the plain shape areas and their inertia values.

You can download and review the content of this post through the following pdf file.

For an external resource, Engineering core courses, the moment of inertia.

This is a link to my ‘1-Moment of Inertia – English’ video on YouTube.
This is the next post, Product of inertia Ixy– for the right-angle triangle-case-2.