Last Updated on December 31, 2025 by Maged kamel
Product of inertia Ixy-for the right-angle triangle-Case-1.
Step-by-step guide for the calculation of the product of inertia for the right-angle triangle-Case-1.
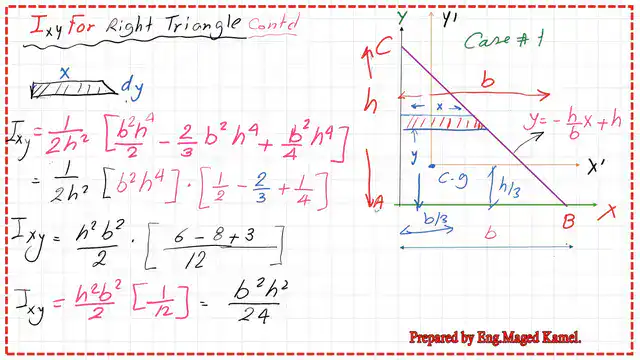
1-For the product of inertia Ixy estimation, a horizontal strip will be used. The strip width is dy, and its height is x from the external axis X, which passes the triangle base.
Since the strip height starts from the base and intersects with line Bc, the y value of the strip is the same y value for the equation of line BC. y=-h/b*x+h.
We can check the equation by substituting the values of x =0 and x=b and check whether this y value is satisfied or not.
2- The moment of inertia due to that strip = dA*xcg*ycg, our xcg x/2, while ycg = y.
3- We will substitute the value of dA, which is (x*dy), and try to make all our items a function of y, since we will integrate from y=0 to y=h, for the Ixy value.
We have x^2=(b^2/h^2)(y^2-2yh+h^2), we can substitute this value and readjust the terms. dA=xdy, dIxy=xdy(x/2)y=(1/2)x^2y dy.

4-After performing the integration, the summing of items will be continued for the matched items. The following slide illustrates the guide to get the final values for the product of inertia.

Finally, we get the value of the product of inertia- as Ixy=h^2*b^2/24 about the x and y axes intersecting at the left corner A. The product of inertia is written as Ixy=(Height^2 by base^2/24). The product of inertia is positive at the corner point.
Product of inertia for a right-angle triangle- Case 1 at the Cg-by using the parallel axes theorem.
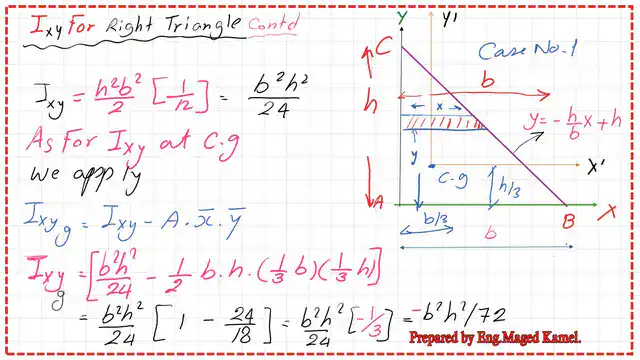
5-For the product of inertia for a right-angle triangle- Case 1 at the Cg, we will use the parallel axes theorem and deduct the product of A*(x-bar)*(y bar) from the product of inertia at the external axis.
The final value of the product of inertia can be estimated by selecting the proper distance for x-bar, which is equal to +b/3. At the same time, the vertical distance to the y bar is =+h/3. The product of A*xbar*ybar=1/2*(b*h)*1/3*b*1/3h=1/18*(b^2*h^2); this value is to be deducted from Ixy.
6- Finally, we get Ixyg=b^2*h^2/24-1/18*(b^2*h^2).=(-)b^2*h^2/72.
The product of inertia for case 1 of the right-angle triangle at the CG is negative. Refer to the next image for more details. The moment of inertia about the CG of a right-angle triangle case-1=(-)*(base)^2*height^2/72.
We can get any value for the product of inertia for any point by adding the product of inertia value at the Cg to the product of the area by the x*y values. Still, for points below the Cg and to the right side, the product of inertia value will be (+ve)*(-ve), which will produce a final negative value. This will apply, for instance, for the line AB at point B.
Point C is above and to the left of the Cg, with x distance= -b/3, while y distance for point C is + 2/3*h; so we expect the product of inertia to have a negative value.
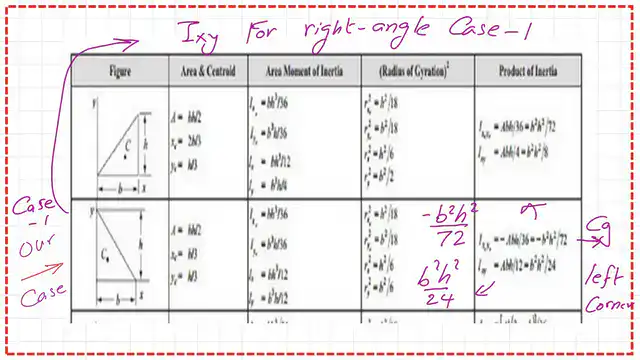
There is a negative sign in the expression for the product of inertia Ixy at the Cg of the triangle. Please refer to the following slide image for the ixy values for right-angle triangle -case 1.
As we can see, the final result matches the values included in the table of inertia for plane shapes.
You can download and review the content of this post through the following pdf file.
This is a link to the Second Moment of Area for Standard shapes.
For the next post 10: Ix-the moment of inertia for right-angle-Ix-Case-2.