9b- Practice problem: longitudinal weld of a plate section

Last Updated on September 9, 2026 by Maged kamel

Practice problem: longitudinal welds of a plate section.

This is a Practice problem on longitudinal welds of a plate section. This is case 4 for the shear lag factor table D3.1-CM-14. It can also be considered case 4a based on CM-15 and the related specification -2016.

In this post, we present two solutions: the first based on CM-14 and the second on CM-15.
A 3/8″x 55 x 5″ plate section of A36 steel with two longitudinal welds, as shown in Figure P3-34, is required to determine the LRFD and ASD values, neglecting block shear.

The weld Area is 3.75 in^2; see the next slide for details.

Estimate the shear lag factor U based on CM-14.

As shown in the next picture, Table D3.1 presents shear lag factors for connections to tension members. For longitudinal welds, it is case 4. Here, it is only for plates where longitudinal welds transmit the tension load. The shear lag factor depends on the joint width w and establishes a relation between the connection length L and width W.

1-From the given Data for ASTM A36, we can get the yield stress Fy=36 ksi and the ultimate stress Fult = 58 ksi.

From the given section of PL3/8″x 5″, the width of the plate w=5 inches; we cannot estimate the plate’s minimum shear lag factor by dividing theAreaa of the connected Area by the whole Area, since it is not allowed by the code for plates.

2- The given section gives the connection length equal to 5 inches.

3- From the given section of PL3/8×5, the width of plate w=5 inches .

4- There are three cases based on the relation between L and W for the value of shear lag factor U. For this practice problem, we have L=W, and the U value will equal 0.75.

The equations we use for LRFD and ASD design.

Effective Area based on CM-14.

The net Area of the longitudinal weld of a plate section is equal to the gross Area of the plate, which is (width by thickness)=5×3/8=1.875 inch2.

The effective Area is found by multiplying the U*net Area, which equals 1.406 in^2.

Estimating the Nominal strength for a practice problem: longitudinal weld of a plate section.

We have two cases for the nominal strength. The first case is tensile Yielding, for which we consider the full Area. Tensile strength equals the yield stress multiplied by the Area and can be found as (1.875*36) = 73.125 kips.

The second case for tensile strength is rupture strength, which equals the effective Area multiplied by the ultimate stress; it can be calculated as (1.406*58) = 81.55 kips.

LRFD strength for practice problem: longitudinal weld of a plate section.

Multiply the first value of the strength due to yield by the reduction value of φ equal to 0 .90; we can get the LRFD strength due to Yielding as equal to 60.75 kips.

When we multiply the second value of the strength due to rupture by the reduction value of φ, which is equal to 0.75, we can get the LRFD strength due to rupture, which is equal to 61.16 kips.

We select the lower value as the final LRFD strength, 60.75 kips, indicating that Yielding governs.

ASD strength for Practice problem: longitudinal weld of a plate section.

Multiply the first value of the strength due to yield by the reduction value (1/Ω) equal to (1/1.67); we can get the ASD strength due to Yielding as equal to 40.42 kips.

Multiply the second value of the strength due to rupture by the reduction value (1/Ω) equal to (1/2), and we can get the ASD strength due to Yielding as equal to 40.78 kips.

We will select the lower value as the final ASD strength, which is 40.42 kips. This indicates that Yielding governs the ASD strength.

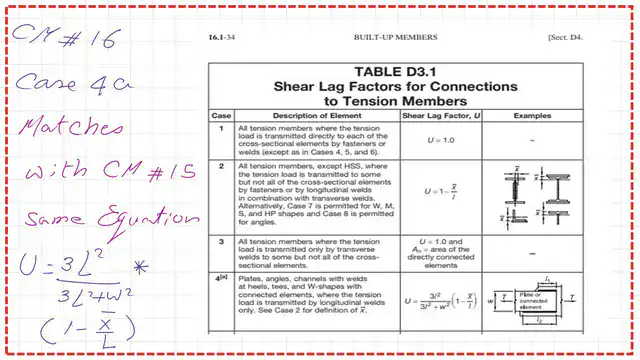
Estimate the shear lag factor U based on CM-15.

Refer to Table D3.1 for the shear lag factor based on CM-15. The item number for the shear lag factor U for a longitudinal weld to a plate is 4a. It includes other structural items with longitudinal weld links, as in the previous version of Table D3.1 for Cm-14.

The U value is estimated by the Product of (3L^2/3l^2*w2) multiplied by (1-1- x̅/ L). The second term equals 1 for plates.

1-From the given Data for ASTM A36, we can get the yield stress Fy=36 ksi and the ultimate stress Fu = 58 ksi.

From the given section of PL3/8×5, the width of the plate is w = 5 inches.

1- The given section gives the connection length equal to 5 inches.

2- From the given section of PL3/8×5, the width of plate w=5 inches .

3- The shear lag factor U equals(3*5^2/(3*5^2+5^2)=0.75 which is the same value as estimated by CM-15.

Effective Area based on CM-16.

For item 4a, CM-16 does not change from CM-15. Please refer to the following slide image for more details.

The estimation of the effective Area for CM-15.

The net Area of the longitudinal weld of a plate section is equal to the gross Area of the plate, which is (width by thickness)=5×3/8=1.875 inch2.

The effective Area can be found by multiplying the U*net Area, which is 1.406 in^2. The gross Area is 1.875 in^2.

LRFD strength for practice problem: longitudinal weld of a plate section.

Multiply (0.90*36*1.8) to find 7; the LRFD strength due to yielding, which equals 65.75 kips.

Multiply (0.75*58*1.406); the LRFD strength due to rupture equals 61.16 kips.

We select the lesser value as the final LRFD strength, which is 60.75 kips. This indicates that rupture governs the LRFD strength.

ASD strength for the practice problem: longitudinal weld of a plate section.

From the estimated calculation, the selected ASD value is 40.42 kips; the full data is shown in the next slide image.

You can view or download the PDF file for this post from the following link.

The next post is 9c- Practice problem-longitudinal weld of a C-section.

For a more detailed illustration of block shear, there is a very useful external link to Chapter 3, Tension Members—a Beginner’s Guide to the Steel Construction Manual, 14^th ed.

Chapter 3 – Tension Members– A Beginner’s Guide to Structural Engineering is a great external resource—a Beginner’s Guide to the Steel Construction Manual, 15^th ed.

A useful external link: Tensile Yielding and tensile rupture. A Beginner’s Guide to the Steel Construction Manual, 16^th ed.