Plastic Nominal Uniform load for partially loaded beam.
We will make an adjustment to the solved problem included in the previous post, by making the uniform load occupies half the length of the span but from the left side.
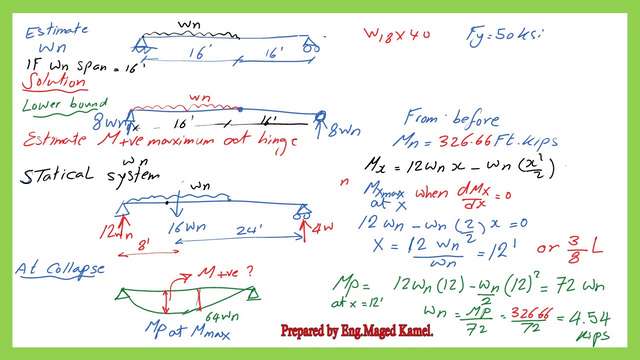
For the steel beam that has a section of W18x40, with the yield strength Fy=50 ksi, it is required to estimate the Plastic Nominal Uniform load for partially loaded beam, Wn Value in this case.
For the positive bending moment, we want to check the location of the maximum moment point in order to locate the plastic hinge accordingly.
We have RA= 12*Wn, while RB=4*Wn, since the total load=Wn*16, RA=16*Wn*/(32-8)/32=12*Wn.
RB=4*Wn, we will estimate the moment as a function of and then differentiate with respect to x.
Solving the modified example by the lower bound theorem.
The moment value at the edge can be estimated as equal to the product of the right support reaction by the arm and can be written as RB*16=4*Wn*16=64*Wn, this is a linear relation.
The left portion is in the form of a parabola.
The point of maximum moment is located where the sum of shear forces is equal to zero.
We have a second method to get the position of a point with the maximum moment, by differentiation.
Let x is the distance from the left support. We will estimate the moment at a point that has a distance x from the left support. The moment at x, Mx=12*Wn*x-W*x^2/2.
We will differentiate with respect to x, and set dM/dx=0. After differentiation we have, 12*Wn-Wn*x=0, x is found=x=12′ or 3/8*L, where the span length L=32′.
We estimate the plastic moment as M-plastic=Mx at x=12′, Mp=12*Wn*12-Wn*(12)^2/2=72.0*Wn.
We have a given section of W18x40, use a table to get Zx, the plastic section modulus for that section, Zx value=78.40 inch3.
The Nominal Mn= Mp=Fy*Zx=50*78.40 inch. kips, then divide the value of Mp by 12 to convert it into Ft.kips.Mn=Mp=50*78.40/12)=326.66 Ft.kips. From m the relation Mp=72*Wn, we can get the value of Plastic Nominal Uniform load Wn.
Mp=326.66 ft. kips. Wn=Mp/72=326.66/72. Plastic Nominal Uniform load Wn=4.54 kips/ft.

Solved problem 8-32 using the upper bound theorem.
For the same modified problem, to estimate the Plastic Nominal Uniform load for a partially loaded beam, we will create a mechanism, and the same procedure to be followed.
The partial loading can be considered as the sum of two cases, the first case where the span is under full load acting downwards minus the case where partial loads act upwards.
The plastic hinge is located at the place of the maximum moment at x=12′ from the left support.
The deflection at that point is delta Δ, the angle at A due to that deflection=θ, and the angle at support B is θ1.
The internal work=Mp*(θ+θ1). θ=tan θ=Δ/12, while θ1=tan θ1=Δ/20.
For the external work=We1=0.50*Wn*32*Δ, then We1=32*Wn/2-We2, we will estimate the deflection value at the edge, which has a distance of 16′ from support B, the value of Δc can be estimated from Δc/Δ=16/20, Δc=0.80*Δ.
We estimate the average for the deflection at point C, Δc, which is 0.40*Δ. The value of We=Wn*Δ*16-Wn*16*0.40*Δ, We=16*Wn(1-0.40)=9.6*Wn*Δ.
For the internal work Wi=Mp*(θ+θ1), θ+θ1=(Δ/12)+(Δ/20)=32*Δ/240.
We=9.60*Wn*Δ)=Mp*32*Δ/240. Wn=32Mp/(2409.60), Wn=32326.66/(2409.60)=4.54 kips/ft. We can find the value of the Plastic Nominal Uniform load is equal to 4.54 kips/ft.


We get the same value of 4.54kps/ft as the Plastic Nominal Uniform load for the partially loaded beam from both the lower and upper bound methods are identical.
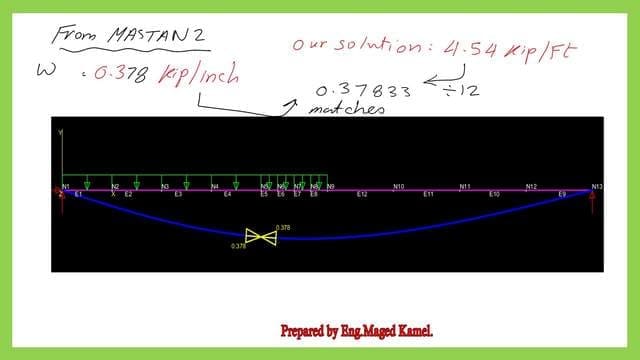
Solving the modified example by MASTAN 2.
The Partially loaded beam under a uniform load has been solved by Mastan, using 1.0 kips/inch and using increments but at load equals 0.378 Kip/inch a plastic hinge is formed at 144 inches from the left support. The value of 0.378 kip/inch matches our solution of 4.54 kips/ft.

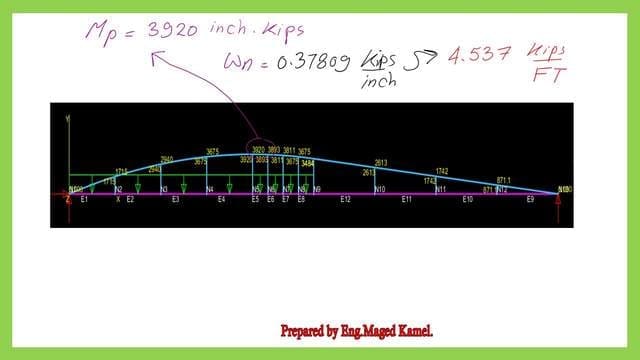
In the next slide, we can see the Bending moment diagram for the Partially loaded beam, and we note that the Plastic moment value is 3920 inch. kips which is the value of 4.537 kips /ft.

This is the pdf file used in the illustration of this post but without MASTAN 2 additional data.
Have more information about the structural analysis –III.
The next post is Solved problems 8-33&34 for a nominal uniform load.

