Last Updated on August 8, 2024 by Maged kamel

solved problem-7-4-1-part 2. 

This is the second part of the solved problem 7-4-1, where it is required to design a W section for a given beam with a span of 20 Feet. The steel is A572, where Fy=65 ksi.

For Case-3, design a steel beam with Fy=65 ksi. Solve the problem: 7-4-1-part 2.

Find the Ultimate Moment for the given beam.

The following slide includes the value of the ultimate load without considering the beam’s weight, which will be added after selecting the section. The ultimate load is 1.52 kips/ft, and the ultimate moment is 76 ft. kips. The beam’s flange is fully supported against lateral movement.

We will equate the ultimate moment with the φb*Mn or φb*Fy*Zx.the Fy=65 ksi, φb=0.90, Mu=76 Ft.kips.

Determine the required Zx-select a section.

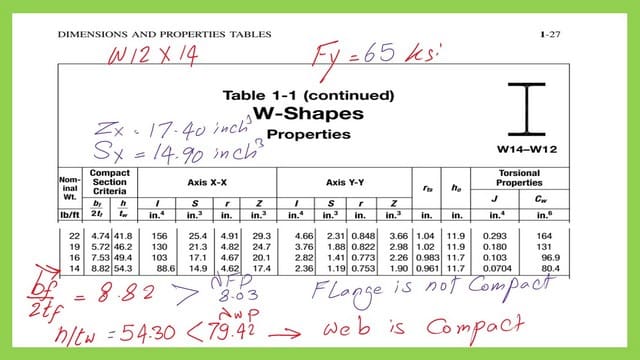
The required Zx value is 15.589 inch3. Using Table 3-2 for W sections sorted based on Zx, we will select a W12x14 with a Zx value of 17.40 inch3, Zx selected > Zx required. Please refer to the next slide image for more details.

We need to check whether W12x14 meets the requirement of local buckling parameters. The next slide shows the controlling parameters for the flange and web.

What are the local buckling parameters based on Fy=65 ksi?

Based on Fy=65 ksi, the lambda for flange at plastic stage λFp=8.03. The lambda for flange at elastc stage λFr=21.12. The lambda for web at plastic stage λwp=79.42. The lambda for flange at elastc stage λwr=120.40. The next slide shows the detailed estimate and the corresponding values for Flange λ and Web λ based on Fy=65 ksi.

Check flange λ and web λ against local buckling parameters.

In the second part, we use Table 1-1 for W12x14 to find the value bf/2tf, which equals 8.82, while h/tw equals 54.30. if we check, we will discover that bf/2tf is bigger than λFp but smaller than λFr, which means that the flange is non-compact. For λw is smaller than λwp, meaning the web is compact. So the entire W section will be considered as non-compact.

The Nominal Moment for W12x14 is between the value of (Fy*Zx) and (0.7*Fy*Sx). The elastic section modulus Sx=14.90 inch3, while the plastic section modulus Zx equals 17.40 inch3.

Find the Nominal moment of W12x14.

For the next slide, the flange lambda value λF =8.82,Fy=65 ksi.

Our λf=8.80, in between λf-p and λf-r. It is required to get the Mn value.From Equation F3-1, Mn=(Mp-(Mp-0.70Fy*Sx)/(λfr-λfp)). This is the last step of designing a steel beam under Fy=65 ksi.

Mn is the same as the equation for a straight line y=m*x. We will estimate the Mn for the upper  Point, which equals Mp=Fy*Zx=65*17.40=1131 inch. Kips. The second point Mn=0.70*Fy*Sx, Sx for the section=14.90 inch2.
0.70*Fy*Sx=0.70*65*14.90= 677.95 inch. Kips.

Find the slope of the Linear portion.

We can find the slope of the linear portion, which equals (Fy*Zx-0.70Fy*Sx)/λfr-λfp). The next slide shows the slope’s value as 34.61-inch. Kips.

Now, we can find the Nominal moment equal to Mp-S*(λf-λp)=1103.66 inch. Kips. We can find the value in Feet Kips as 92.0 ft. kips. The Φb value is 0.90. the factored Mn=82.80 Ft.kips.

We will finalize the ultimate moment value by adding the W section’s own weight moment. The final Mu value is 77.0 feet. KIPS. The Φb*Mn=83.00 feet. Kips. The section is safe since Φb*Mn>Mult. This is the end of the post. Thanks a lot.

For the first part of this post, please refer to post 8: How to design a steel beam? Solved problem-7-4-1.

Here is the link for Chapter 8 – Bending Members.
This links to the next post, 9b-Practice problem 5-4-1-Check compactness for Fy=60 ksi.