Last Updated on August 31, 2024 by Maged kamel

Practice problem 5-4-1-Check compactness for Fy=60 ksi.

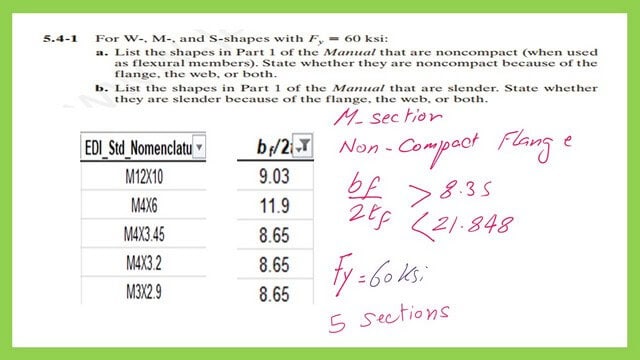
Practice problem 5-4-1 For W-, M-, and S-shapes with Fy = 60 ksi: the first part a. List the noncompact shapes in Part 1 of the Manual (when used as flexural members). State whether they are noncompact because of the flange, the web, or both.
b. List the shapes in Part 1 of the Manual that are slender. State whether they are slender because of the flange, the web, or both. Practice problem 5-4-1 is from the Steel Design Handbook.

List the W, M, and S shapes based on compactness when Fy=60 ksi.

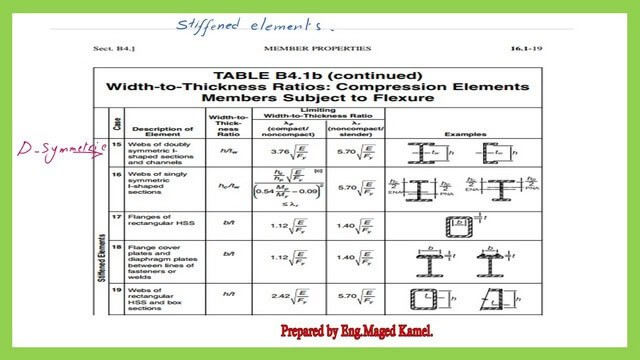
The three steel sections, W, M, and S shapes, follow item 10 in Table B4.1b for the lambda value for the unstiffened flange. For the web compactness h/tw, these sections follow item 15 in the same table,

The following slide shows the main difference between W, M, and S shapes in the profile as I section. W shape has a slope of 2:12 and a broader flange width. The S shape has a slope of 6:1 and is available in a smaller range. The M stands for Miscellaneous beams.

Determine the values of compactness ratios for Fy=60 ksi.

Based on item 10 in Table B4.1b, the flange λFp=0.38*sqrt(E/Fy), since we have E29000 ksi and the given Fy=60 ksi, then λFp=0.38*sqrt(29000/60)=8.35. λFr=1.0*sqrt(E/Fy)=1*sqrt(29000/60)=21.964.

for the web compactness ratio, the flange λwp=3.76*sqrt(E/Fy), λWp=3.76*sqrt(29000/60)=82.66. λwr=5.70*sqrt(E/Fy)=5.70*sqrt(29000/60)=125.31. Please refer to the next slide image for the detailed estimate of compactness ratios.

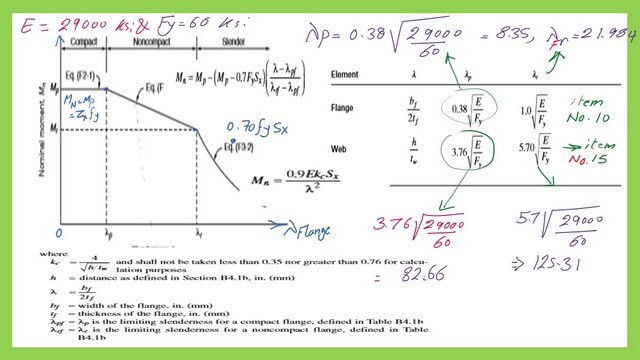
Table B4.1b details stiffened and unstiffened elements.

The next two slides show the details of items 10 and 15 for compactness ratios for members subjected to flexure.

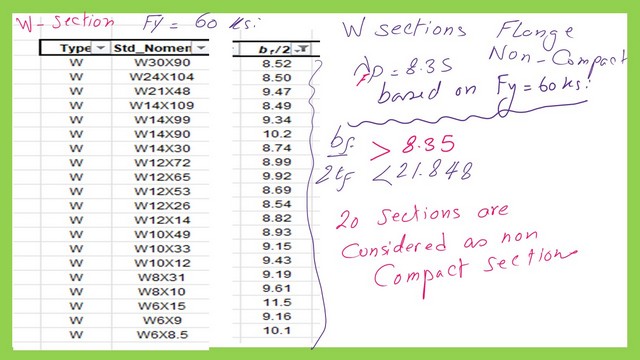
Sort W sections based on bf/2tf>λFp but less than λfr.

We will use an Excel sheet for Table 1-1 for W sections and sort W sections with bf/2tf bigger than 8.35, which is the value of λFp, but smaller than 21.848, the value for λFr. These are the non-compact sections for steel, with Fy=60 ksi.

The total number of W sections is 20, starting from W30x90 and ending with W6x0.50.

The next slide image shows the detailed dimension of these non-compact W shapes.

Find the non-compact web for W sections based on Fy=60ksi.

There is no non-compact web for W sections based on Fy=60 ksi; the maximum h/tw for W30x90 is 57.50, smaller than the value of λwp, 82.66.

What are the tables for properties of M and s sections?

The next slide shows the tables used to find the properties of W, M, and S shapes. We use Table 1-1 for W sections, and for M sections, we use Table 1-2. For S shapes, we use Table 1-3.

Sort M sections based on bf/2tf>λFp but less than λFr.

We will use an Excel sheet for Table 1-2 for M sections and sort M sections with bf/2tf bigger than 8.35, the value of λFp, but smaller than 21.848, the value for λFr. These are the non-compact sections for steel, with Fy=60 ksi. We have only five non-compact sections, starting from M12x10 and ending with M 3×2.9.

Find the non-compact web for M sections based on Fy=60ksi.

There is no non-compact web for M sections based on Fy=60 ksi; the maximum h/tw for M12.5×12.40 is 74.80, smaller than the value of λwp, 82.66.

Sort S sections based on the flange and web compactness ratio.

e will use an Excel sheet for Table 1-3 for S sections and sort S sections with bf/2tf bigger than 8.35, which is the value of λFp but smaller than 21.848, the value for λFr. There are no non-compact S sections for steel, with Fy=60 ksi. As for the ratio h/tw, there are no non-compact S shapes for the web.

Part b-Sort W, M, and S sections are based on slender sections.

Based on Fy=60 ksi, the W, M, and S sections do not have slender sections. We have reached the end of our post. Thanks a lot.

Here is the link for Chapter 8 – Bending Members.
This links to the next post, 10-lateral-torsional buckling for steel beams.

There is a newly added post, which is a practice problem 5-5-6-Compute Lp and Lr and φb*Mn.