9- Easy approach to Area and Cg for a Parallelogram.

Last Updated on September 8, 2024 by Maged kamel

Area and Cg for a Parallelogram.

Reference handbook 10.00 value for area and Cg at the x-direction.

To get the area and Cg for a parallelogram, we will divide the parallelogram into a rectangle and two triangles and consider taking the first moment of area about a vertical axis y passing by the external edge point about the external axes. This will give the x-bar of the parallelogram.

As for the Y bar, we will do the same process, but the first moment of the area will be taken about an external axis passing by the base which is then called the x-axis. it is required to get the same data as obtained from the FE reference handbook as attached in the next slide image, for case #No.6.

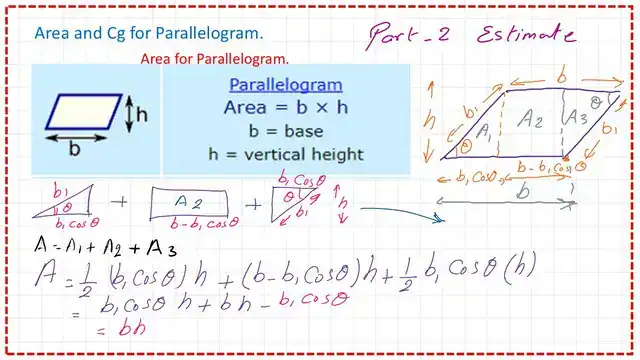
Area and Cg for a parallelogram at the x-direction.

To get Area and Cg for a parallelogram at the x-direction. we will check the base b and height h- is and then we divide it into the following shapes:

1-A left triangle of base (b₁cos θ) and a height of h, its area A2=1/2*( b₁cos θ)*h, its CG is apart from the y-axis by a distance x1=(2/3*(b₁cos θ).

2-A rectangle of base (b-b₁*cos θ) and a height of h, its area A1=(b-b1*cos θ)*h, its CG is apart from the y-axis by a distance x2=1/2* (b+b₁*cos θ).

3-A right triangle of base b₁*cos θ and a height of h, its area A3=1/2*b₁*cos θ*h, its CG is apart from the y-axis by a distance x3=(b+1/3*b₁*cos θ).
We will simplify the expression by adjusting the different terms, the area will be=b*h as a skewed rectangle. The next two slide images give the full details of the estimation.

The area of the Parallelogram is the Area of the left triangle+area of the rectangle+ area of the right triangle, The details of these shapes are shown in the next slide images.

x₁,x₂, and x₃ values are shown in the next slide image.x₁ is the first triangle Cg distance to the y-axis. Similarly, x₂ is the Cg distance for the rectangle shape about the y-axis.x₃ is the x distance for the third shape from the Y-axis.

The first moment of areas for these three shapes will be = the first moment of area for the Parallelogram about the Y-axis.

The final value for area and Cg of a Parallelogram at the x-direction.

We will have the final expression for the distance of the Cg of the parallelogram about the y-axis, which is the X-bar. The next EFUNDA will show the same expression but considered as a- instead of a.

Area and Cg for a parallelogram at the y-direction.

The parallelogram with base b and height h, is divided into the following shapes:

1-A left triangle of base (b₁cos θ) and a height of h, its area A2=1/2*( b₁cos θ)*h, its CG is apart from the x-axis by a distance y1=(1/3*h).
2-A rectangle of base (b-b₁*cos θ) and a height of h, its area A1=(b-b1*cos θ)*h, its CG is apart from the x-axis by a distance y2=1/2*h.
3-A right triangle of base b₁*cos θ and a height of h, its area A3=1/2*b₁*cos θ*h, its CG is apart from the X-axis by a distance Y3=2/3h.

The area of the Parallelogram is the Area of the left triangle+area of rectangle+ area of the right triangle, The details of these shapes are shown in the next slide images.

After adjusting the various terms we will have Y bar =h/2. the expression in terms of a will be used as h=b1*cos θ.

To get the expression for the Rectangle, we will consider θ as=90 degrees. For the Moment of inertia Ix for a parallelogram, please find the link.

This is a link to the previous post. We have estimated the area and CG for a trapezium.

Please refer to the practice problem for the x and Y coordinates for a given Trapezoidal area

ُEfunda gives a useful link for areas, and Cg can be viewed.