Last Updated on September 23, 2026 by Maged kamel
How to use the Newton-Raphson method for structural analysis?
The Newton-Raphson method can be used to perform a structural analysis of a supported Beam under a uniformly distributed Load to determine its maximum Deflection. Two approaches will be used. The first approach uses the Newton-Raphson method.
The second approach will use the modified Newton-Raphson method.
Revisit the Newton-Raphson method-The first approach.
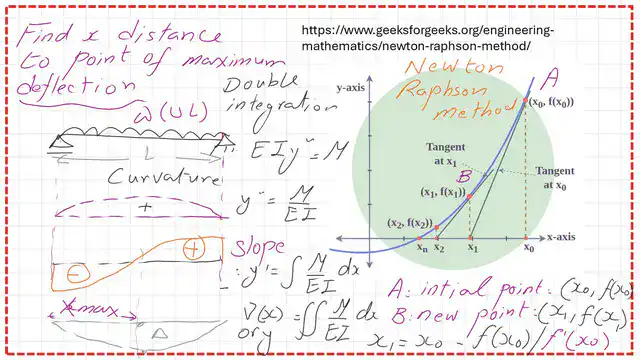
First, we have the y-axis, which is located at the left support Point. Select Point A, a distance X0 from the y-axis, and draw a tangent at Point A on the graph of f(x). That slope intersects the x-axis at a Point with a horizontal distance of X1 from the y-axis.
Then we will either measure or calculate the corresponding Value of Y, or f(x1), for that Point.
We repeat the process from Point B to get Point B’; then we draw a slope at B’, and the slope hits the X-axis again at a Point we call C.
We are looking for the Point with a y-value of 0. We estimate the y-value and repeat; we take several steps, which is why we approach the root of the y-value.
The Point of maximum Deflection for a Beam under Uniform loading.
As a direct application of this method, for a uniformly distributed Load, for example, after structural analysis we obtain a Deflection curve and identify the Point of maximum Deflection, which corresponds to the x-coordinateof the left support.
Here, for that curvature of the Deflectionwe don’t have an intersection of the dDeflectioncurve with the X-axis except for x=0 or x = LL; that’s why we cannot directly use the Newton-Raphson method with that Expression of x1 = x0-(f(x0)/f'(x0) to get the distance to the Point of maximum Deflection.
We use theBeamm’s slope graph to apply the Newton-Raphson method.
The slope at the maximum Point of Deflection will be 0, or the slope curve intersects the X-axis. That’s why, when checking the slope (y’) curve, we find that the zero Point, or root, is at the same distance, Xmax, from the left support.
Thus, we use the y’ curve as the primary curve to perform a structural analysis of a Beam and determine the distance to the maximum Deflection.
In the next slide, we will see a graph for the Expression of Newton-Raphson: x1 = x0- f (x0)/f'(x0), which deals with Y as f(x) when the y-curve intersects with the x-axis.
But in our case, the Y’ curve intersects the x-axis. Now our root Point is on another curve, which is y’, the slope curve for the uniformly distributed Load on a supported Beam, which is a function of x ‘.
Accordingly, the Newton-Raphson method’s terms will be modified, as shown in the next slide. Based on the Newton-Raphson Method, x1=x0-f(x0)/f'(x0), while we were dealing with Y as a function of X.
Now our root Point is at another curve, which is y’, that’s why we are going to replace the original Expression, for instance, f(x0), with f ‘(x0) and f'(x0) Value by f”(x0).
The double integration method Expression, or elastic curve, is y”=M/EI, while ywherewherethe slope, and it can be calculated by integrating M/EI. The Expression for y, the Deflection, is given by double integration of M/EI.
Let us see how we can proceed using the y’-slope curve.
First, select an arbitrary X0 distance; this is your starting Point. The slope from the left-hand side is negative,, so we will aestimate f'(x0).
This Time we draw a curve. We draw a slope at that Point, then hit the y-curve at another Point, which is different from x1. The same procedure we have done earlier: for that x1, we are going to estimate y’ at the x1 Point for the f ” (x0). We then proceed to the curve of y”, and we get the corresponding f ”(x0).
Using the Modified Newton-Raphson method.
As a second approach using the modified Newton-Raphson method for the structural analysis, the Expression of the equation will be modified as:
Replace f(x) with f'(x), and f'(x) with f ” (x). How are we going to get f ” (xi)? By recalling the Expression that y ”, which is a curvature variation, is =M/EI, when you are going to differentiate d2v/dx2, accordingly, you will differentiate M/EI, so for d3V/dx3= (dM/dx)/ y/EI, Expression. We are familiar with the dM/dX, which is the Shear diagram; that’s why d3v/dx3 = Q/Ei.
A practice Problem: a Beam under a concentrated Load.
I added a new practice Problem to illustrate the idea, rather than using a Beam with a Uniform Load, since we already know the maximum Deflection Point is at the middle. I selected a Beam with a Point Load, as we will see next. Based on the analytic solution, using Macaulay’s function, the distance to the Point of maximum Deflection is 8.165m from the left support.
The expressions for Load, ShShShear, Moment, Slope, and Deflection are discontinuity functions.
In the following slide, we can see the details of the Load, Shear, Moment, Slope, and Deflection expressions for the given Beam. However, for the region between a and b, we do not use the expressions marked in green, as they are valid only for x > 10m.
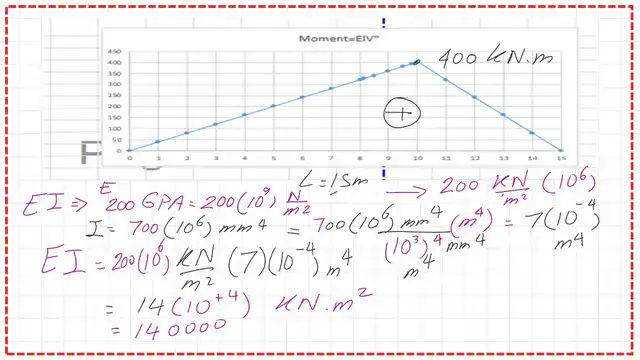
The maximum Value is 400 kN · m at a distance of 10m from the left support. For EI, it is equal to 14*10^4 kN·m^2.
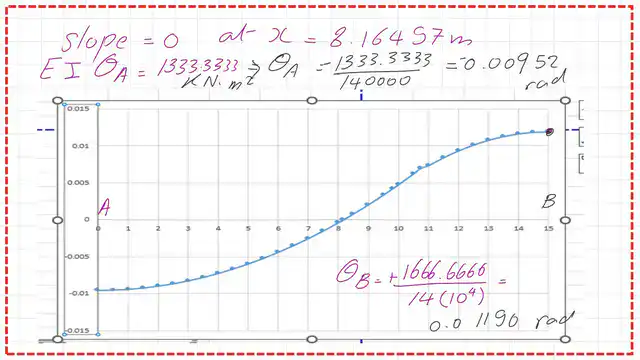
The following slides show the graphs of slope and Deflection for the given Beam.
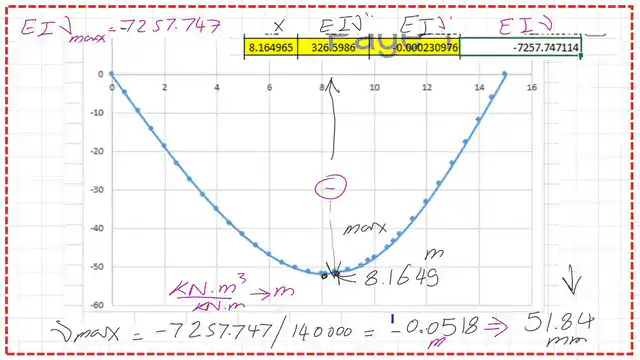
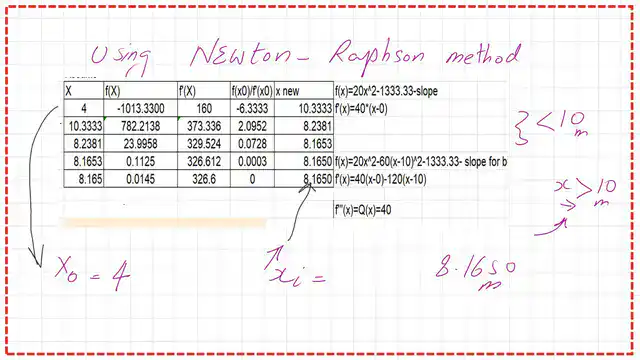
Use the Newton-Raphson method to get the Point of Maximum Deflection.
As indicated, we will use EI*v’, or the slope function, as f(x) in the Newton-Raphson method, and f'(x) will be the EI” function, which is the Moment M(x) of the Beam. Our initial guess is x0 = 4.00 m. The Point of the maximum Moment is between A and B, so we do not use the Expression for (x-10).
The Value of x1=x0-(EIV'(X0=4.00)/EIV”(X0=4)). We estimate EIV’ and EIV” at x0 = 4 m and substitute them; we get X1 = 10.3333 m, which is greater than 10.0 m.
The following slide shows the estimation of EIV’ and EIV values for X1=10.333 m. We use the full Expression since x > 10 m, and we find x2 = 8.2381 m.
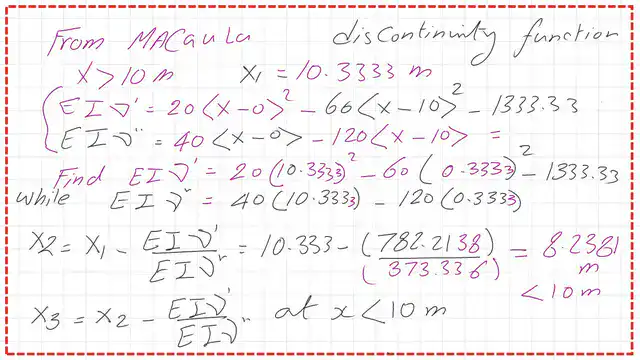
The Value of X3 is 8.165m, which matches the figure obtained by the analytical method.
A Table of different values of xi, from x0 = 4.00 m to x4 = 8.165 m, based on the Newton-Raphson method.
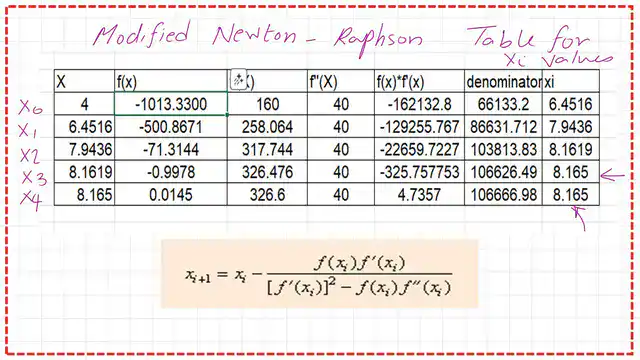
Use the modified Newton-Raphson method to get the Point of Maximum Deflection.
In the following slide, we show the Load, Shear, bending Moment, slope, and Deflection expressions for the given Beam. However, for the region between a and b, we do not use the expressions marked in green, as they are valid only for x > 10m. The Shear V(x) is expressed as EIV”.
We will start with an initial vValueof x0 = 4.0 m, but to apply the Modified Newton-Raphson equation, we need to find the Shear Value Q(x) as EIV”, EIV’ as F(x), and EIV” as M(x). The Value of X1=6.4516 m.We will use an Excel sheet to find the various values of Xi.
This is the last slide for estimating Xi using the modified Newton-Raphson method to find the Point of Maximum Deflection; for x4, the Value equals 8.165 m. Thanks a lot.
You can review or download the data for this Post from the following Link.
The next Post will include a solved Problem applying this method. The next Post Link is the Maximum deflection distance by the Newton-Raphson method.
This Link is useful for a numerical analysis calculator.