7A-Solved problem-8 by Modified Newton-Raphson method

Solved problem-8 by Modified Newton-Raphson method.

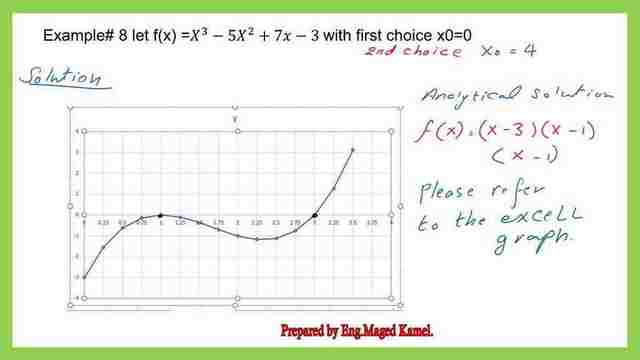
For the given Solved problem-8 by the Modified Newton-Raphson method. The function f(x)=X^3-5*X^2+7x-3 with the first choice of x₀=0.

Again I make a graph by plugging different values and getting the corresponding values of f(x), I have started from x=0 to x=3.50.

From the graph, as we can see from the next slide image, the roots are three roots x1=3 & x2=1 and x3=1 as shown in the Excel sheet for the Solved problem-8 by Modified Newton-Raphson method. the x=0 will give a negative value of -3.

1-We start to use the modified Newton-Raphson method, consider the initial point x0 equals 0, and we start to find the expressions for f(x),f'(x) , f’^2(x), and f”(x) .
2- Substitute at x=0 and get the values for f (0), f'(0) & f’^2(0), and f”(0). The value of f(0)=-3. The value of f'(0)=7.

The value of f”(0)=-10. Substitute in the equation of the modified Newton-Raphson method, we get the value of x1, which will be =1.105. Please refer to the next slide image for a detailed estimation of the various parameters.

We plug in with the value of x=1.105263 and get the corresponding values of f(1.105263),f'(1.105263), and”(1.105263).

4- Substitute in the modified Newton-Raphson method. We get a new point with x2=1.00. and again continue to estimate f(1.00) and f'(1.00) and then apply them in the equation to get a new point that will be point x₃.

5-Continue the process until x converges to 1.00. The Excel sheet for the various values of x, based on the modified Newton-Raphson method from x₀=0 till x₄=1.00 is shown.  

This table shows how many iterations and the corresponding f(x),f'(x), and f”(x) for each case. 

   

Solved problem-8 by Modified Newton-Raphson method using x₀=4

Now if we consider the starting point as x₀=4.00, and proceed to get the x value for f(x)& f'(x) , f’^2(x) and f”(x) for x0=4.00. We have f(4)=9,f'(4)=15 and f”(4)=14. The value of x1 is found to be=2.6363.      

2- Substitute at x₁=2.6363 and get the values for f (2.6363), f'(2.6363)  & f”(2.6363). the values are shown in the next slide image.

3-Plug in with previous calculation to the Modified Newton Raphson equation and d out the value of X2 Substitute at x₂=2.8202 and get the values for f (2.6363), f'(2.8202)  & f”^2(2.8202)  and f”(2.8202) and get the value of x₃, it will be=2.9617.

This is the Excel sheet for the calculation based on the Modified Newton Raphson Method starting from x₀=4 till x5=3.00.

Solved problem-8 by Newton Raphson method with x₀=0.

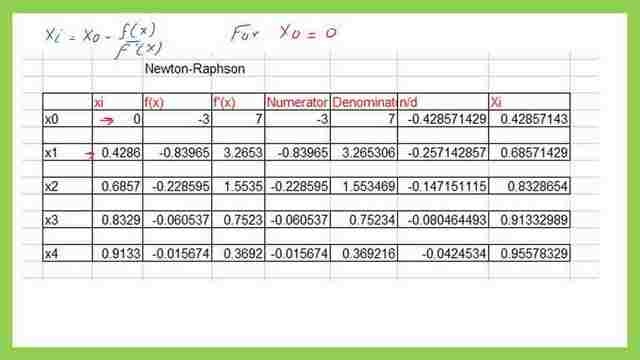
This is a comparison by the Newton Raphson method without modification for the same problem-8 but based on the Newton formula. Starting as before with x0=0 and using the equation of xi=x0-(F(x0)/f'(x0), we can get the x1 value 0.4285, then substitute and get the x2 value=0.6857.

This is an Excel sheet for the points that are obtained by using the Newton-Raphson method for the Solved problem-8

The initial point is (0) the table lists all the values of the function till point x4. That point will be equal to 0.95578.

If we start with x₀=4.00 to get the other root but based on the Newton-Raphson method. The Excel sheet with more details shows the different values of x.

This is an Excel sheet for the points obtained while considering the initial point x₀=4.00 ending with point x6 with a value of 3.

This is a comparison between the Newton Raphson and Modified Newton Raphson methods for the same solved problem-8 using an Excel sheet.

This is the PDF file used for the illustration of this post.

The next post is Structural analysis numerically by the Newton-Raphson method.

This is a useful link for a numerical analysis calculator.