Last Updated on September 9, 2026 by Maged kamel
A solved problem 4-2 for shear Lag factor U for a welded connection.
We continue together with the shear lag factor; how do we evaluate it? We will look at the solved problem-4-2, from Abi Aghayre, from the structural steel design version 3; the solved problem concerns the weld for one leg of an angle.
Next are the cases for tensile Yielding and tensile rupture, and how we get the LRFD and ASD tensile design strength.
This is the Grade of steel and the corresponding Fy, Fult values for A36, fy=36 ksi, fult=58-80 ksi, A572 grade,fy=50 ksi, A572 grade, the value of tensile point=65 ksi.
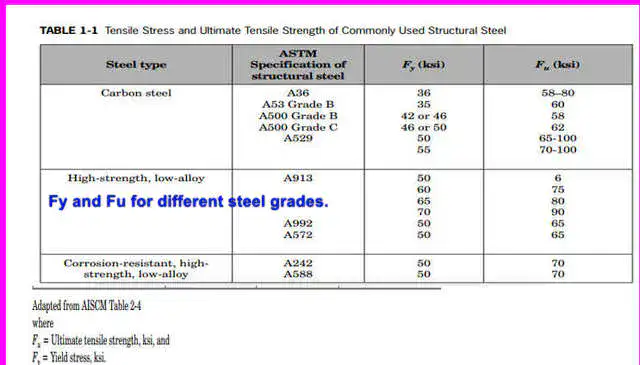
These tables are from the latest revision of AISC-360-16, which we are using to estimate the shear lag factor U. The first table for plates explains the three plate cases.
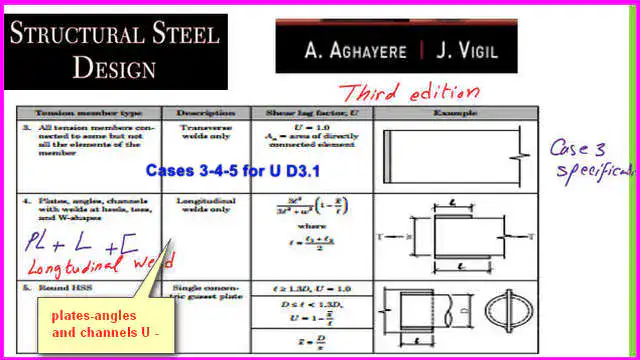
Case No. 3 is the case of any tension member welded to another element by a transverse weld, for which the U value is 1.00.
Case No.4a: In this case, a plate, angle, C channel, and angle are welded in the longitudinal direction only in tension to another element, for which an equation gives the U value to estimate the U value.
These are the various rectangular connection cases to a single plate or to two plates, along with the corresponding values for each.
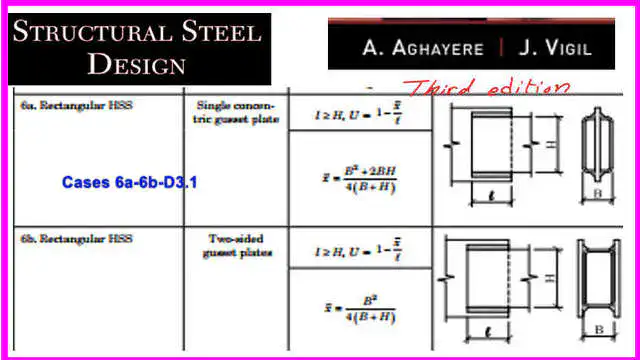
The next slide shows the U-value for a rectangular HSS for connections to a single gusset plate and to two gusset plates.
Cases 7 and 8 for the W section and angles, with different connection types and their U values.
How do we estimate the weld length when weld lengths are unequal?
On page 53 of Prof. Segui’s book, if you have a Tension member that is welded in one leg with a plate in the vertical direction, as shown,n as well as welded at the longitudinal top and bottom edges for the other leg, whether it has an equal weld distance for both the upper and lower portions, or different top and bottom side distances, for which L1 is the weld length for the upper part of the leg with the plate and L 2 is the length of the weld for the lower portion of the leg.
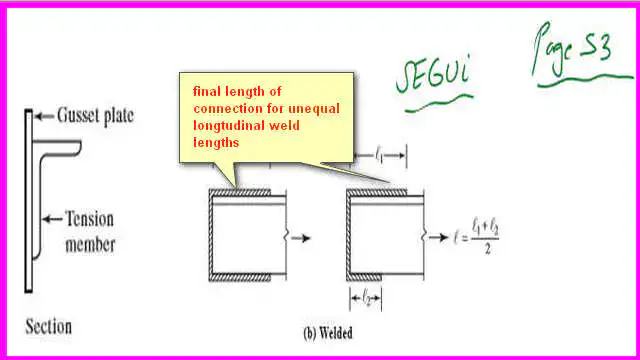
From Commentary 16-1, page 303, for a welded connection, L is the length of the weld parallel to the line of force. Here, as shown, the different weld lengths are in the direction of the force. In Fig.. CD-3.4, for longitudinal and longitudinal-plus-transverse welds, L is the length parallel to the force.
For different lengths, use the average length, which is the focus of problem 4-2 on shear lag.
Solve problem 4-2 for shear Lag factor U.
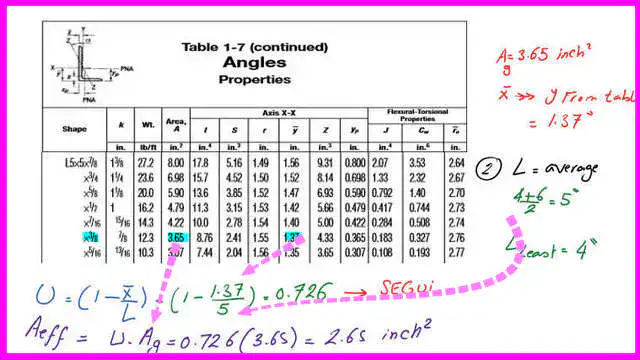
Evaluate the U value for the welded connection angle L 5x5x3/8 on three sides. Since one leg is not connected, the U value is less than 1. The lower weld length is 4″, and the upper weld length is 6″. The upper leg is welded at the edge with a length equal to the angle height. It is not connected to the backplate.
The steps to follow are: first, determine x̅ and the Area of the angle. We have an angle of 5x5x3/8″, for which the Area is =3.65 inch2. he x̅, which is y̅ value from the table=1.37″
The connection length, L, is the average of the upper and lower weld lengths: 6″ and 4″, respectively.
L=0.50*(4+6)=5″. The U value equals(1- x̅/L=(1-1.37/5)=0.726.The net Area equals the gross Area since no bolts are used. The effective Area is (0.726 × 3.65) = 2.65 in^2.
The following post contains two solved problems on effective net Area.
You can view or download the PDF for this post from the following document.
For a more detailed illustration of block shear, there is a very useful external link to the Tension Members chapter 3—aBeginner’s Guide to the Steel Construction Manual, 14th ed.
Chapter 3 – Tension Members —A Beginner’s Guide to Structural Engineering is a great external resource: A Beginner’s Guide to the Steel Construction Manual, 15th ed.
A useful external link: Tension Yielding and tensile rupture. A Beginner’s Guide to the Steel Construction Manual, 16th ed.