7b- Practice problems for Gauss Jordan elimination.

Practice problems for Gauss Jordan elimination.

Practice problems for Gauss Jordan elimination-first practice problem.

We will introduce a practice problem Gauss Jordan elimination, or the reduced echelon form. Practice problem number #33 is from Stewart’s book College Algebra.

For the first practice problem #33 for Gauss Jordan elimination. Solve the following systems of linear equations. The detail of the given matrix for practice problem #33 is shown in the next slide image.

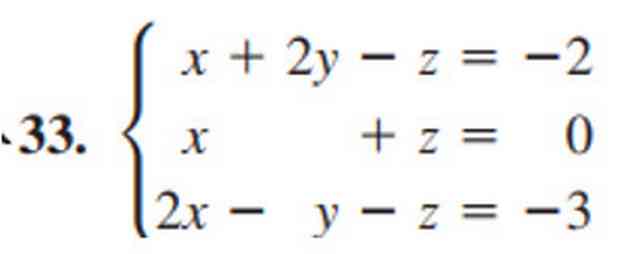
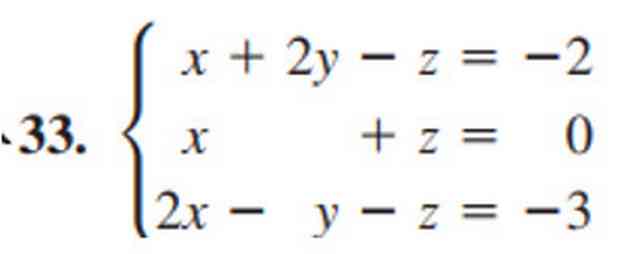
Practice problems for Gauss Jordan elimination a11 as a pivot to eliminate a21 and a31.

For the given system of linear equations, we will write these equations in augmented form.

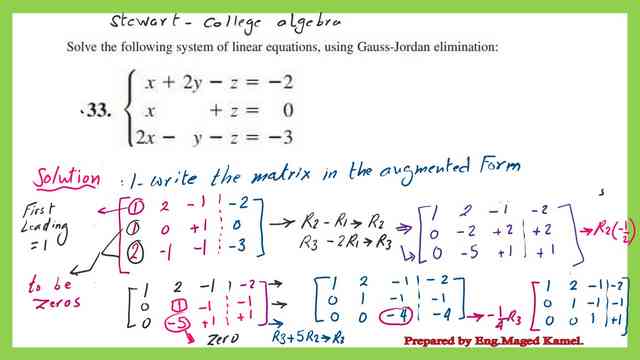
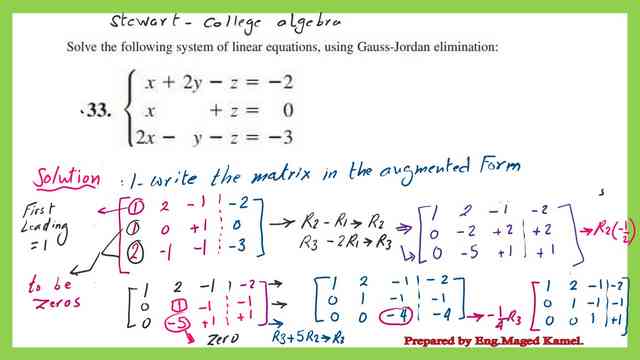
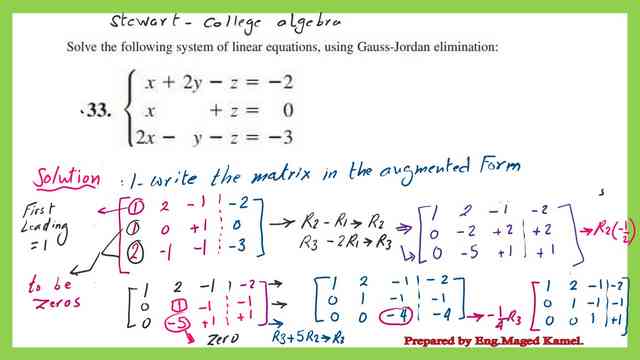
We will introduce a vertical line between the third column and the fourth column to show the augmented matrix. The next step is to let a21 or the second row/first column be equal to zero. Make sure that the element a11 is equal to 1, then add (-a21/a11)*R1 to row2 to get the zero value. In this process, we consider a11 as the pivot element.

Similarly, let a31 or the third row/first column be equal to zero. This is done by adding (-a31/a11)*R1 to row 3 to get the zero value. Again, in this process, we consider a11 as the pivot element.

carry on the row operations. Make sure that element a22 is equal to 1, this is done by multiplying row 2 by (-1/2).

Use a22 as a pivot to eliminate a32.

Use a22 as a pivot by adding R3 to -(a23/a21)*R2. Perform the row operation to get the reduced echelon form or simply an upper matrix with three ones as diagonal.

Refer to the slide image to check the necessary row operations to get the reduced row echelon form of Gauss elimination.

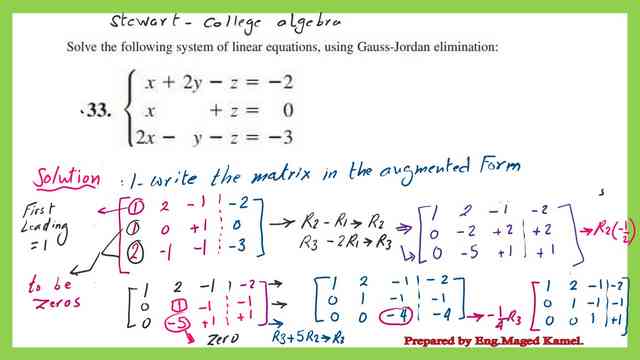
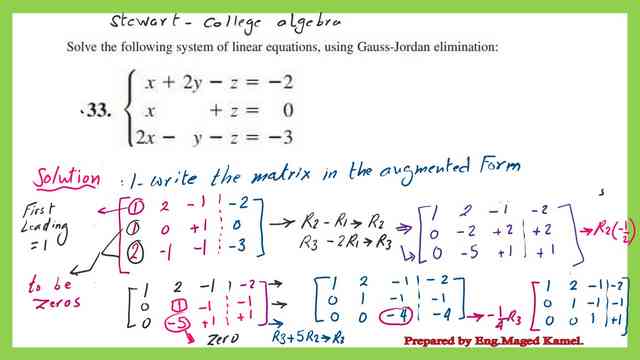
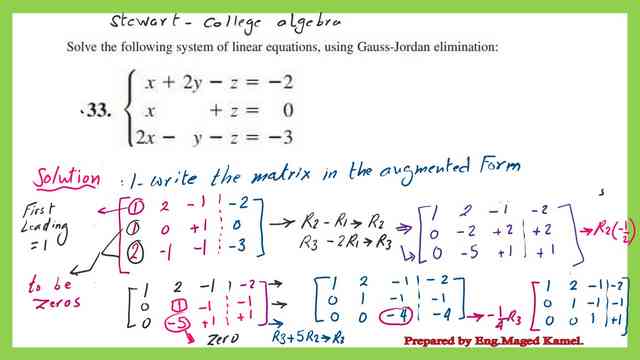
Use a33 as a pivot to eliminate a23& a13.

We aim to convert the matrix to a diagonal matrix of 1’s. We will use the element a33, to eliminate a23, this is done by adding(-a23/a33)*R3 to R2.

Similarly, we use the element a33, to eliminate a13, this is done by adding(-a13/a33)*R3 to R1to get the zero value. Again, in this process, we consider a33 as the pivot element.

Use a22 as a pivot to eliminate a12.

We will use the element a22, to eliminate a12, this is done by adding(-a12/a22)*R2 to R1. Now we have obtained the required diagonal matrix with 1 at the diagonals, please refer to the next slide image for clarity.

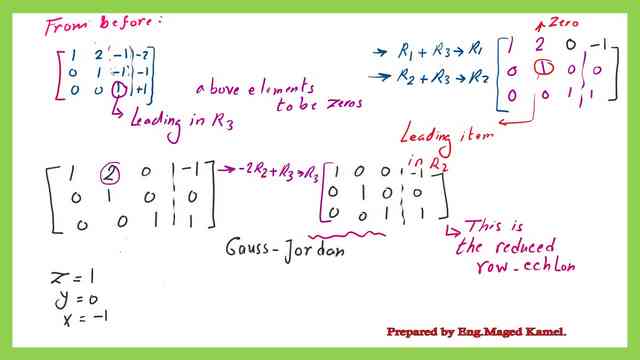
We can then get the values of Z=1&Y=0 and X=-1. In this method, we do not need to make back substitutions. It is important to check the Values of X& Y and Z in any of the three systems of equations to make sure that the solution is accurate.

Practice problems for Gauss Jordan elimination-second practice problem.

1-For the second practice problem #38 for Gauss Jordan elimination. Solve the following systems of linear equations. The detail of the given matrix for practice problem #38 is shown in the next slide image.

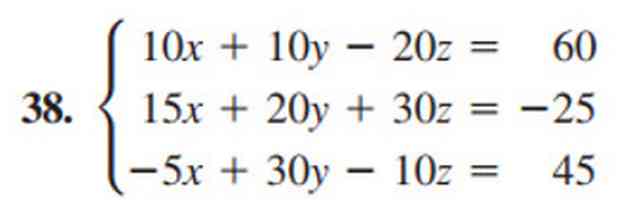
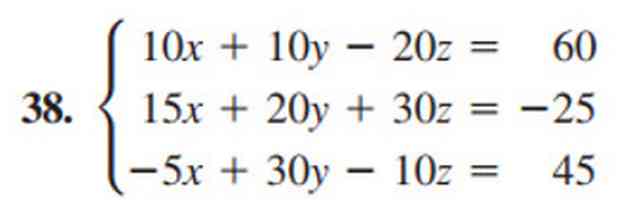
For the given system of linear equations, we will write these equations in augmented form.

We will introduce a vertical line between the third column and the fourth column to show the augmented matrix. The next step is to let a21 or the second row/first column be equal to zero.

Make sure that element a11 is equal to 1. First, we will divide the first row by 10. We will add (-a21/a11)*R1 to row 2 to get the zero value. In this process, we consider a11 as the pivot element.

Similarly, let a31 or the third row/first column be equal to zero. This is done by adding (-a31/a11)*R1 to row 3 to get the zero value. Again, in this process, we consider a11 as the pivot element.

Use a22 as a pivot to eliminate a32.

First, divide R2 by 5 to let the pivot a22 equal 1; also, divide r3/5 to minimize the numbers.

Use a22 as a pivot by adding R3 to -(a23/a21)*R2. Divide r3 by 7 to let a33=1.

Perform the row operation to get the reduced echelon form or simply an upper matrix with three ones as diagonal.

Use a33 as a pivot to eliminate a23&a13.

Our aim is to convert the matrix to a diagonal matrix of 1’s. We will use the element a33, to eliminate a23, this is done by adding(-a23/a33)*R3 to R2.

Similarly, we use the element a33 to eliminate a13; this is done by adding(-a13/a33)*R3 to R1 to get the zero value. Again, in this process, we consider a33 as the pivot element. Now we have obtained the required diagonal matrix with 1 at the diagonals, please refer to the next slide image for clarity.

We can then get the values of Z=-2&Y=1 and X=+1. In this method, we do not need to make back substitutions. It is important to check the Values of X& Y and Z in any of the three systems of equations to make sure that the solution is accurate.

In the next post, we will discuss the Practice problems for reduced echelon form.

This is a link to the matrix calculator.

For a useful external link, math is fun for the matrix part.