Practice problem for REF-The first part.
Practice problem for reduced echelon form-REF.
In the first part of the post, we will introduce Practice problems for reduced echelon form. or abbreviated as REF. There are several parts a,b,c, and d.
For the first practice problem, it is required to check which matrices are in reduced echelon form and justify the reason for
Part a-practice problem for reduced echelon form.
In the first part, part a, of the Practice problem for reduced echelon form, we have three pivots, each equaling 1. The three are located in the first, second, and third rows. We have zeros below the first pivot.
There are zeros above and below the pivot in the second column. While for the third column, there are two zeros above the pivot. These conditions satisfy the requirement of the reduced row echelon form shown in the next slide image.


Part-b- practice problem for reduced echelon form-REF.
In the second part, part b, we have only two pivots, each equaling 1, which can be considered a non-zero element. The two ones are located in the first and second rows. We have zeros below the first pivot.
There are zeros above and below the pivot in the second column.
These conditions satisfy the requirement of the reduced row echelon. For the third row, there is no leading entry. These conditions satisfy the requirement of the reduced row echelon form shown in the next slide image.


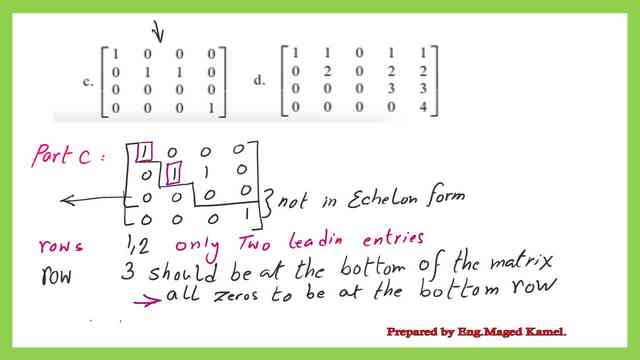
Part C-practice problem for reduced echelon form.
In the third part, part c, of the Practice problem for reduced echelon form, we have only two pivots, each equaling 1, which can be considered a non-zero element. The two ones are located in the first and second rows. We have zeros below the first pivot.
There are zeros above and below the pivot in the second column. In the third row, we have zeros. In the last row, the pivot is not leading. The given matrix is not in the reduced echelon form since the row of the zeros should be placed as the last row
.

Part d-Practice problem for reduced echelon form.
In the fourth part, part d, of the Practice problem for reduced echelon form, we have only one leading pivot as one in the first row. In the second row, the leading pivot is not equal to 1; it is equal to two, which does not comply with the rules of the reduced echelon form. There is no zero above the a21 element.
The matrix can be considered an echelon form but not a reduced echelon form. The details of the arrangement of the leading pivots are shown in the next slide image.



In the fourth part, part d, of exercise 2 of the Practice problem for reduced echelon form, we have a leading pivot as zero in the first row. This is not acceptable whether in the reduced form of the echelon form. The details of the arrangement of the leading pivots are shown in the next slide image.



Traffic flow application-the second part.
The application for traffic flow is the second part of the post. We have a practice problem with the distribution of the traffic for the various intersections.
The traffic flows are expressed in the form of linear equations based on the in and outflows for every joint.
The main principle is that the sum of inflows is equal to the sum of outlaws. Based on the given data at joint A, the sum of entering=x1+450, while the sum of outgoing is x2+610.
We can write accordingly the equations for points B&C and D. The details of the given incoming and outgoing joints or intersections are shown in the next slide image.


We can rearrange a set of linear equations for the four joints of intersections and find values of the unknowns x1&x2&x3 and x4.
We can turn the augmented matrix into echelon form by a series of matrix operations. The detail of the echelon form of the four equations or intersections is shown in the next slide image.


We can further proceed to perform the reduced echelon form and arrange the pivots. We have basic variables and, accordingly three pivot columns. we have a free variable X4, which can take any value. The last row has the equation of zero equal to zero.


We can rearrange the relations between the four variables and write the general equations that show that x4 is a free variable.X1&x2&X3 are the basic variables.
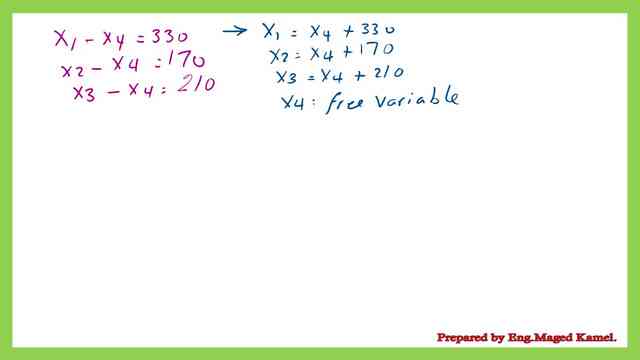
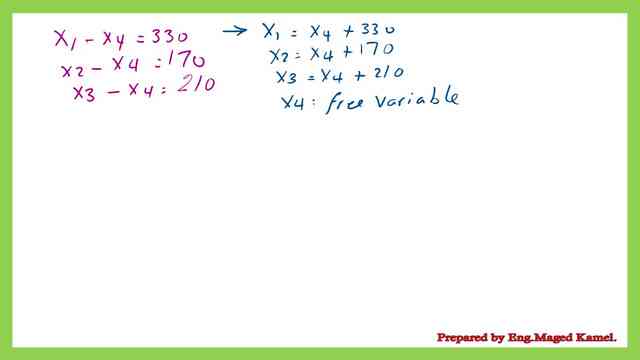
This is a link to the next post titled 9- How to Use a Matrix for the quadratic function?
This is a link to the matrix calculator.
For a useful external link, math is fun for the matrix part.

