Last Updated on July 15, 2025 by Maged kamel
Uniform series of compound interest-2/2 in the Economy.
Solved example 4-1, how to determine the F value in terms of P, A, and I%?
In compound interest-2/2, we take a look at Solved Example 4-1 from Prof. Donald G. Newman’s book, Engineering Economic Analysis.
A man deposits $500 in a credit union at the end of each year for 5 years. Our timeline starts from 0 to 5. The deposits were made over 5 years, at the end of years 1, 2, 3, 4, and 5. The final value, or F, is the future value to be estimated, which is cash from the person’s point of view.
Solution: this example is a direct application of the uniform series.
The symbolic form of the future value can be written as F value=F*(A/ F, i%,n), where f is the required future value,n is the time in years, and A is the amount of uniform series. I is the interest rate yearly.

We have the interest i=5%, the uniform series value A=$500, and n=5. Then the future value can be estimated as F=A*((1+i)^n-1)/i. F=500*((1+0.05)^5-1)/0.05=(500)*0.27625)/0.05. F=$2763, this is the future money that will be received after 5 years.

Solved example 2.5, how to determine the F value in terms of P, A, n, and I%?
The solved example is from Profs Leland Blank’s and Prof. Anthony Tarquin’s book of Engineering Economy.
Example 2.5 The president of Ford Motor Company wants to know the equivalent future worth of a $1 million capital investment each year for 8 years, starting 1 year from now.
Ford Capital earns at a rate of 14% per year. The author uses $1000 units, for F/a the author has estimated the value as (1+0.14)^8-1/0.14=1.852586/0.14= 13.2328 by the author. F=1000*13.2328 =$13,232.8 in units, estimated when i%= a compound interest %14.
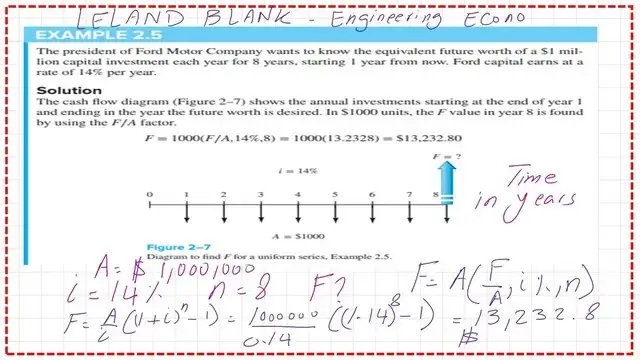
If we wish to estimate the future value F by relation, given the present value p=1000 and an interest rate i=14%, we have F=1000*(1+0.14)^8-1 divided by I. The future value of the uniform series F=1000* (1/0.14) * (1+0.14)^8-1=$13,232.0, which is the same value as estimated by the author.
Solved example 4.3, how to determine the A value in terms of P, n, and I%?
The Solved example is from Prof. Donald G Newman’s book, Engineering Economic Analysis. Solved example 4.3 explains how to estimate the uniform series of compound interest.
Example 4.3 Consider a situation in which you borrow $5000. You will repay the loan in five end-of-the-year payments. The first payment is due one year after the loan is received.
The interest rate on the loan is 8%. What is the size of each of the five payments?
Solution:1- We draw the timeline from 0 to 5, the cash in at time t=0, where P= $5000, but the loan will be repaid in series with an equal amount.

2. The first payment is due after one year, with a 5-year term and an interest rate of 8%. We have 5 payments in years 1, 2, 3, 4, and 5.
3-This relation is not a relation between A&F but between P and A.
4-A value= F(i/(1+i)^n-1), since F=P*(1+i)^n. We adjust the relation to be A=P*(1+i)^(i/((1+i)^n-1)).
5-We have (1+i)^n= (1+0.08)^4.
The value of A can be found in the following equation. A=5000*(0.08)*(1.08)^5*(0.0.08/((1.08)^5-1)=$1252. Please refer to the following slide image for more details.

The following post title will be post 8- Easy Illustration of the Arithmetic Gradient. The post includes an easy illustration of a new type of cash flow, which is the arithmetic gradient series cash flow, which involves an increase or decrease of a constant amount in the cash flow of each analysis period.
For a valuable external resource, Engineering Economy is a good reference.