Last Updated on January 8, 2024 by Maged kamel

Introduction to row echelon form or REF.

Our subject as of today is the row echelon form. We are using the row matrix operation to create a new form which is the RE form. The following steps are explained:

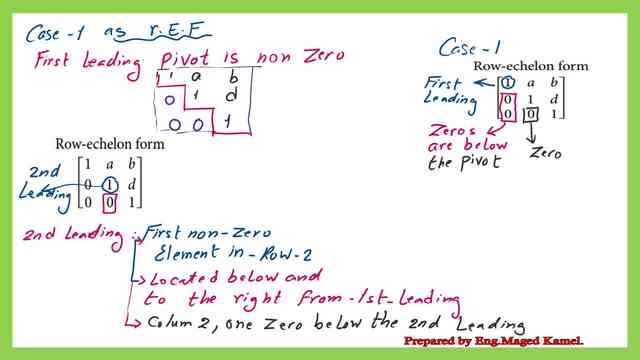
1-For the first row of the first item, the first row/first column is called the leading item, which must be equal to 1.

2-For the first column/2nd row and third row, all the elements are zeros.

2-For the second row, the leading item which is 1 will be below and to the right of the previous row’s leading item, as we can see the number 1 is the second row/2nd column position. Put a zero below the leading item in the third row.

For the third row, we expect to have a leading I as in the third column. This is one definition for the RE form Quoted from Steven Leon’s book Linear Algebra with Applications.

But other authors, state that the leading item is to be non-zero items that conclude that the number could be 1 or any positive value.

Please refer to the wiki for the RE form for more information. The details of the RE form and how to create are shown in the next slide image and the two definitions are indicated.

These are the three items for the REF which stands for the free echelon form based on the leading item to be nonzeros. All rows of zeros should be the last row at the bottom.

What is the RREF?

The RREF stands for the reduced row echelon form, this form has the three previous items included in the RE form but all leading entries must be 1s. The column that has the first leading one should have zeros below it. While the columns of the leading ones should include zeros above and below the leading ones.

This is the case of a matrix with a 3×3 dimension in the REF. We have a diagonal that contains three ones, the leading items are nonzero values. The first leading one has two zeros below the leading item.

This is the case of a matrix of a dimension of 3×4 in the augmented form. We have a diagonal of nonzeros items, shown as ones. The solid boxes include any possible values.

The pivot column in matrix A is the location that corresponds to the leading items. In the shown matrix we have three leading ones, which means that we have three pivot columns.

The use of the RREF to solve a system of linear equations.

The RREF echelon form is the method used by Gauss-Jordan to get the solution of linear equations, to avoid the back substitution method.

Step 1:Create a RE form by using row operations.
Step 2: Use the leading term in the third row to create a zero for the elements above it.
Step 3:Use the leading term in the second row to create a zero for the element above it.

Based on these operations, the values of the fourth column will be changed, and at the end, we can get the value of the unknowns directly.

For instance, if we have the following system of linear equations as x+y+z=6 & 2x-y+z=5 and 3x+y-2z=9.

Perform row operation to create an RREF, we will get the arranged augmented matrix.
This new arrangement will give us the values of x=3, y = 2, and z = 1. There is no need to use the back substitution to get these values.

Another example for the REF.

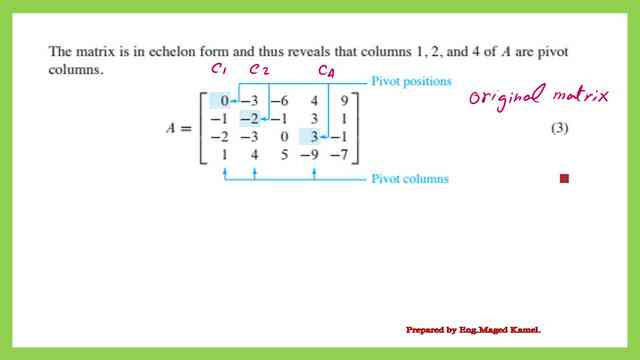
In the given matrix A of a dimension 4×5, it is required to perform row reduction to the matrix and locate the pivot columns.

The first row has a leading term of zero, which can’t be accepted, so we will replace the first row with row number 4 which has a leading term of 1 and is accepted as the non-zero item.

We will perform a series of row operations to let the items below the first leading item be zeros. The steps used to have the reduced echelon form for a 4×5 matrix. The shape of the reduced echelon form is shown in the next slide image.

We have the third row containing five zeros which we cannot accept and we will swap the third row to the fourth row to match the condition of the REF. The places of the leading items and the pivot columns are shown in the next slide image. the leading terms are 1&2&-5 which are a11 & a22 and a34.

We have used the REF to find the places of leading terms and the pivot column, so we will return back to the original matrix A, with the information that we have in the next slide image.

In the next post, we will have a look at practice problems for back substitution.

This is a link to the matrix calculator.

For a useful external link, math is fun for the matrix part.