Last Updated on March 5, 2024 by Maged kamel
6-Solved problems for the estimation of Moment of inertia.
The First solved problem for a given rectangle.
We will solve our first problem, problem # 1. We have x and y axes as shown in the next slide, and also we have a rectangular section with width=0.40m and the height is 0.60 m. This rectangle is apart from the y-axis by a distance of 0.20 m.
It is required to estimate the following for the given rectangle. the moment of inertia Ix, Kx, the radius of gyration at the x-axis. While for part b, we want to estimate the moment of inertia at the y-axis Iy and the radius of gyration for the y-axis Ky.
We have our X and Y external axes. As we know Ix = Ixg+ the product of area *(y^2).
For the moment of inertia about the CG, for a rectangle section, we have the expression of (b* h^3/12). Then we have this x-axis. We have to add the product of area multiplied by y^2, first our Ix g=b*h^3/12= (0.40*0.60^3/12, which will give us 0.0072 m4.
Our area is estimated as (0.40*0.60), which is equal to 0.24 m2. For item A* y^2, we have A=b*h and y̅ =h/2 All raised to the power of 2. So we have b*h, which is (0.40*0.60)*(h/2)^2,h/2=0.30 divided by 4, giving us the value of 0.0216 m4.
Our required moment of inertia about the x-axis Ix will be the summation of these two items, the first item is estimated as Ixg=0.0072 plus the second item which is ( A*y̅^2), which is equal to 0.0216 adding both values will give us 0.0288 m4.
To determine k^x we will divide Ix by the area of the rectangle.
the value of kx^2 will be equal to Ix/A=0.0288/0.24=3/25, then the Kx value =sqrt(3/25)=sqrt(3)/5.
For part b of the first solved problem, to find Iy add Iyg+A*xbar^2. Iyg=h*b^3/12=0.60*?(0.40)^3/12=0.0032 m4.
Ax^2g=(0.40)(0.60)(0.20+0.50.40)^2=0.0384m4. The final Iy=(0.0032+0.0384)=0.0416m4.
k^2y=Iy/A=0.0416/(0.40*0.60)=13/75. ky=sqrt(13/75)=0.4163 m2.
.
The second solved problem for a given section.
We can consider the L shape as consisting of two rectangles. The first one of width=1.0 m and height = 4 m and the other rectangle, has a width of 2 m and a height is 1 meter, if we join them together, they will constitute an unequal angle with the same width, as we can see Unequal angle 3 by 4 and a width of 1.0m, can be evaluated as composed of two rectangles.
The first one A1 of width 1.0m and height=4.0 m, which is why its area would become(1*4)=4.0 m^2 And its X1 will be=1/2 m. y1 from the x-axis will be. 4 / 2, which is 2 meters. For the second area, we have the A2=(3-1)*.this is the breadth, the height will be 1.0 m, so we have 2=(1*2)=2.0 m^2.
Our X2, measured to the external y-axis, will be (1m+1/2 of the difference between (3-1.0) Which will give us = 2 meters, our y2= 0.50 m.
The Ix for the unequal angle is the summation of Ix for the first rectangle +Ix for the second rectangle.
The moment of inertia Ix2 value of the solved problem.
The final Ix=22.00 m4 which is part a) of the solved problem.
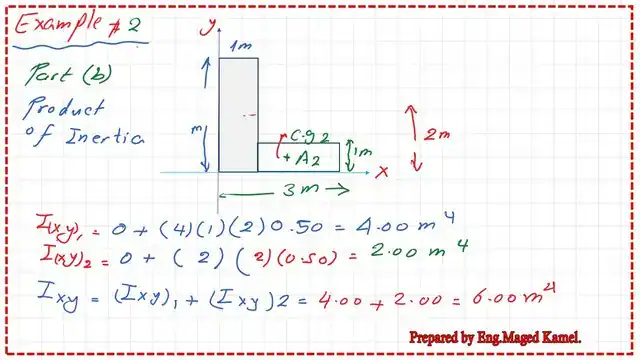
For part c) of the solved problem, we estimate the product of inertia about the external axes for each rectangle and then add them together.
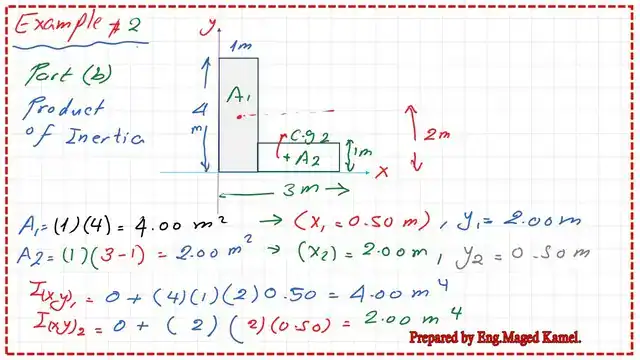
The final Ixy=6.00 m4 is part b) of the solved problem.
This is the PDF used for the illustration of this post.
For the next post, the Moment of inertia for the right-angle triangle-Ix- Case-1.
This is a useful external link for the moment of inertia- The Moment Of Inertia Of Rectangle.