Last Updated on December 17, 2025 by Maged kamel
Permutation matrix.
Our subject will be the introduction to the permutation matrix. A permutation matrix is an identity matrix with rows interchanged.
I have created a YouTube video that covers this post and the next post.
Using this permutation matrix, we can create a new matrix that differs from the old one, with rows rearranged. This is a brief illustration of the permutation matrix quoted from Prof. Mathew W Reid. The author explains that, with the change in the multiplication process, we can obtain either a row swap or a column swap.
First, we start with the identity matrix for a 2×2 matrix. In the identity matrix, we have 1 in the upper left and the lower right corner, and the remaining corners have zeros. Multiplying an identity matrix to a matrix 2xc2 will not change the arrangement of rows or columns.
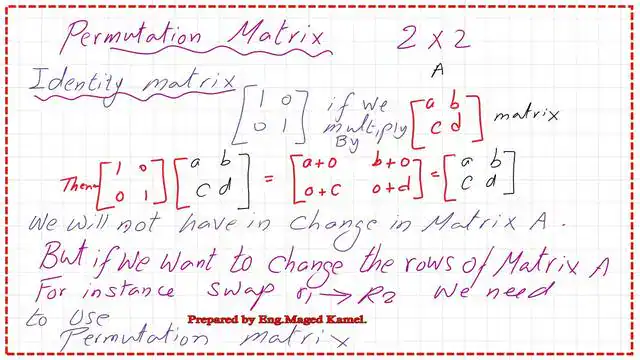
How to swap the first row in a 2×2 matrix?
We have only two options in the 2×2 matrix for swapping rows. The first option is to swap the first row to be as the second row when we multiply a given matrix from the left with a permutation matrix P.
The second option is to swap the second row with the first row in the new matrix. Moving the first row of an identity matrix to the second row and vice versa, then multiplying by another matrix, yields a new matrix with shifted rows, as shown in the next slide.
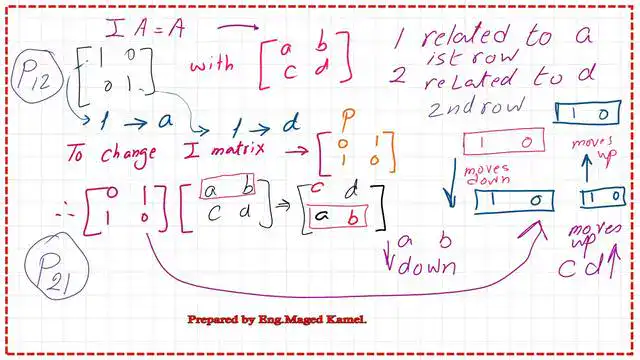
How to swap the first column in a 2×2 matrix?
If we want to change the column arrangement of a matrix, we can multiply it by a permutation matrix whose first column is (0 1). Its second column is (1 0), this arrangement will produce a new matrix arranged as (b a) as a first column and (d c) as a second column. The original matrix arrangement was (a b) as a first row and ( C d) as a second row. Multiplying any matrix from the right by a permutation matrix ( 0 1, 1 0) will create a swap in the columns.
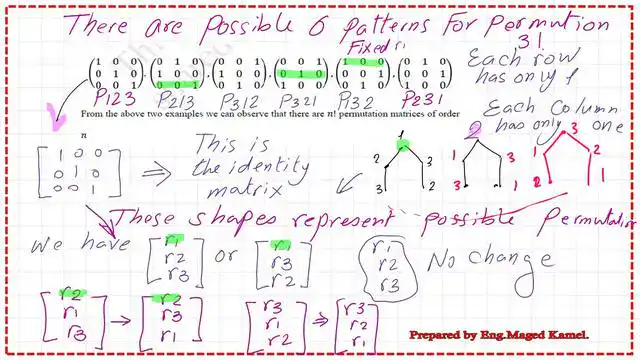
How many permutation matrices are in a 3×3 matrix?
We have (3x2x1)=6 permutation matrices for the 3×3 matrix. 6 sketches showing these arrangements in the next slide image.
The first option is the standard identity matrix I, where row 1 is followed by row 2, and row 3 is at the end. There is an interesting remark about the permutation matrix that it has only one 1 in any of its columns or rows. No more than 3(1s) in the case of a 3×3 matrix. Multiplying the identity matrix by any 3×3 matrix will not change the arrangement of rows.
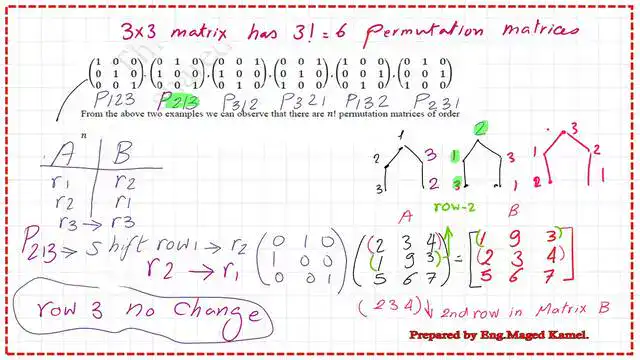
What is a permutation matrix P213?
This is the second arrangement of a permutation matrix (3×3), it is called P213, where there is a swap between row 1 to row 2 and accordingly from r2 to r1, while the third row remains unchanged.
Such a matrix, when multiplied by any other matrix, produces a new matrix in which the first row of the new matrix is the second row of the original matrix, and the second row of the new matrix is the first row of the original matrix.
An example of multiplying a permutation matrix P213 by a 3×3 matrix is shown in the next slide.
The content of this post and the next post can be reviewed via the following PDF file.
This is a link to the next post, which will be post 6a- Permutation matrix-part 2.
This is the Omni calculator for estimating various items of linear algebra -LU Decomposition Calculator.
Link to Omni calculator-LU Decomposition Calculator.
Another calculator to use is Calculator for matrices.