5- What is the Linear Approximation method?

What is the Linear Approximation method?

What is Linear approximation?

Linear approximation, or linearization, is a method we can use to approximate the value of a function at a particular point. There is a reason linear approximation is useful: it can be difficult to find the value of a function at a particular point.

We have a function like that. We know the value of x of a one-point which is called a. We know x_a which is the x-distance, and we know the coordinate value which is f(x=a).

Suppose we have another point, which is considered to be close to point a. We can assume that we have a line tangent to that curve at point a.

We can treat the function as a linear one for any point needed, we get the y value from that line.

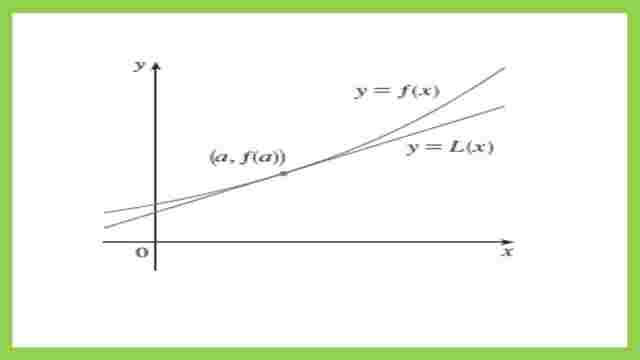
The linear approximation equation.

So the linear approximation actually, is y- the value of any point which we need starting from a given point x_a and its value f(a). We make this line with slope and we just go to another point say c. We get the value of xc by substituting. We get the function value of x_c. 

Linear approximation is a method to get the y value of point b, knowing the value of x of another point called a and its y value.L (x=xb) Is equal to the function value. at a+( the slope of the tangent) *( the difference. Between).
The new Point x_b – the Old Point x_a.

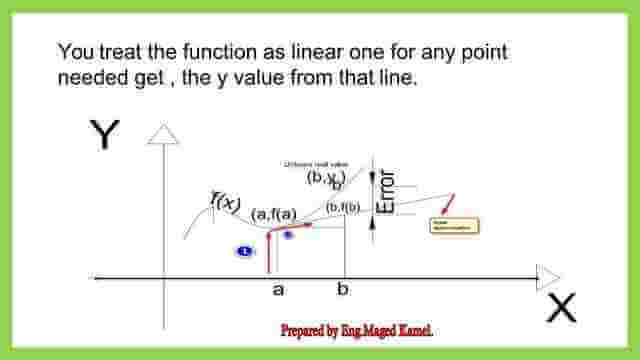
As an application, we can get a linear approximation of any function as well as you can find the power value of a number of the square root of a number or the third root of a number.

Solved problem#2 find the linear approximation of y as f(x)=x^2 at 2.50.

Our solved problem: find the linear approximation of y as f(x)=x^2 at 2.50. We put the equation in the general form by writing. L(x)= approximately=f(x=a)+f'(a) *(x_b-x_a) the difference between point b and point as point a is the starting point for which we know the value of the Y as well as the f’ value.

Our next question what is the nearest Point to 2.50? The nearest point to 2.50 is 2, for which we can get the value of y, as well as, the value of the slope.
 1- We need to estimate the function value at the starting point a, which is equal to (2.0)^2=4.00.
2- We need to estimate the slope value, the x^2 to be differentiated as y’=2*x
3- Get the value of y’ at x=2, it will be=2*(2)=4.0.

4-We can apply the expression and get L(x=2.50) =f(2.0)+(y’*(x_b-x_a), a is the starting point where x=2.0, while xb is the point for which we want to estimate the Y value which is =2.50.
5-The value of L(x=2.50)=4+((2)*(2)*(2.50-2.0))=6.00.
6-The exact value= the approximated value + error, apply in the equation of y=x^2, the exact value is (2.50)^2=6.25, the approximated value=6.00. 7- The error value=6.25-6.0=0.25.

This is the pdf file used in the illustration of this post.
The next post is about the Practice problems with linear approximation.