Last Updated on March 8, 2024 by Maged kamel

Area and Cg for a circular sector.

Reference handbook 10.00 value for the area and Cg for a circular sector.

There is a list of the common round shapes area and CG value. Our fourth case is the case of a circular sector.

You can click on any picture to enlarge, then press the small arrow at the right to review all the other images as a slide show.

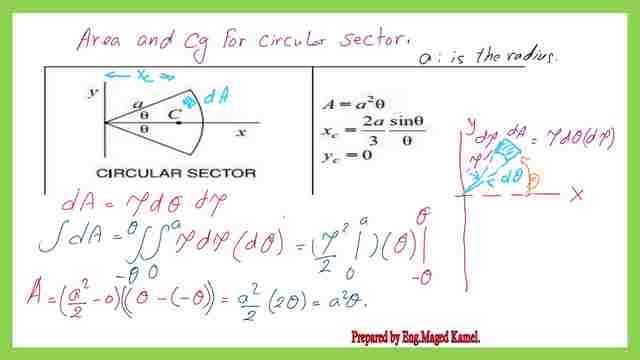
The circular sector is a portion of a circle that is closed by two radii and an arc. Our case will be treated as two radii of length a and the enclosed angle is 2θ.

The external axis Y is passing by the left point of the circular sector which has a radius value of a. The x-axis is Bisecting the angle of the circular sector.

Area and Cg for a circular sector- select an area dA.

We have a circular sector with radius a, for which it is required to get the area and CG. We can find that there’s an internal axis x that divides the circular sector into two similar parts. Due to that symmetry, we expect that the Cg or the center of gravity will be located along the X-axis at a certain distance x from the external axis Y. We have used the radius of the circular sector as equal to a.

The angle θ is the angle enclosed between the Cg of the strip dA with the X-axis. The angle dθ is the enclosed angle by the strip dA.

The circular sector area can be found from the integration of dA= ∬(ρ*dρ*dθ) from ρ=0 to ρ=a and enclosed by an angle equal to dθ. The integration is from θ equals (- θ) to θ=( θ), the final expression for the area is dA=1/2*ρ^2*(θ-(-θ)=1/2*a^2(2*θ)=a^2*θ.

The steps followed to the area for the circular sector is shown in the next slide image.

Area and Cg for a circular sector-first moment of area about the Y-axis.

For the area and Cg for a circular sector about Y-axis. We have two intersecting axes X&Y, we will select a small area dA that has a radius of ρ from the intersection of the two axes X and Y.

The first moment of area for the small area dA about the Y-axis is the product of that area by the horizontal distance to the Y-axis.

The horizontal distance is x, which is equal to ρ*cos θ. The moment dMy=dA*(x)=(ρ*dρ*d θ)*(ρ*cos θ). It will be simplified to (ρ^2*dρ*cos θ*dθ).

For the first moment of area for the whole circular sector, we will use double integration since we have to integrate for ρ from ρ=0 to ρ=a. The second integration is from θ equal to (- θ) to θ equal to (+ θ).

The total value of the first moment of area for the circular sector will be equal to =2*(a^3/3)*(sin(θ-(sin(-θ)=(2*(a^3/3)*sin(θ).

We can find the horizontal distance of the Cg from the Y-axis by dividing the first moment by the area value, this will lead to 2*(a^3/3)*sin(θ))/a^2*θ=(2/3)*(a*sin θ)/θ.

The details of the horizontal value of the horizontal distance of the Cg to the y-axis is shown in the next slide image.

Area and Cg for a circular sector-first moment of area about the X-axis.

For the area and Cg for a circular sector about X-axis. We have two intersecting axes X&Y, we will select a small area dA that has a radius of ρ from the intersection of the two axes X and Y.

The first moment of area for the small area dA about the Y-axis is the product of that area by the vertical distance to the X-axis.

The horizontal distance is Y, which is equal to ρ*sin θ. The moment dMx=dA*(y)=(ρ*dρ*d θ)*(ρ*sin θ). It will be simplified to (ρ^2*dρ*sin θ*dθ).

For the first moment of area for the whole circular sector, we will use double integration since we have to integrate for ρ from ρ=0 to ρ=a. The second integration is from θ equal to (- θ) to θ equal to (+ θ).

The total value of the first moment of area for the circular sector about The X-axis will be equal to =2*(a^3/3)*(-cos(θ-(cos(-θ)=(2*(a^3/3)*0=0.

The vertical distance of the Cg to the x-axis will be=0, which means that the CG point is located along the X-axis.

The details of the calculations for the first moment of area for the circular sector about the X-axis are shown in the next slide image.

We have completed the subject of the area and Cg for a circular sector.

The next post will be on how to estimate the area and Cg for a circular segment.

This is a very useful site: Engineering statics open and interactive.