Last Updated on September 12, 2024 by Maged kamel

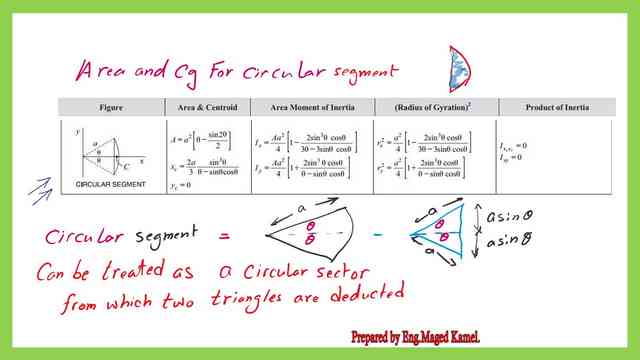
Area and Cg for a circular segment.

Reference handbook 10.00 value for the area and Cg for a circular segment.

There is a list of the common round shapes area and CG value. Our fifth case is the case of a circular segment.

The circular segment is a portion of a circular sector where a cut by a chord is made. Thus the circular sector can be treated as a circular sector from which two triangles are cut. For a circular sector bounded by an angle of 2θ, each triangle has a base of a cosθ and a height of a*sinθ.

To determine the area and Cg for a circular segment, we will deduct the area of the two triangles from the circular sector area.

The details of both the circular sectors and the two triangles are shown in the next slide image. The external axis Y is passing by the left point of the circular segment which has a radius value of a. The x-axis is Bisecting the angle of the circular sector.

Area and Cg for a circular segment.

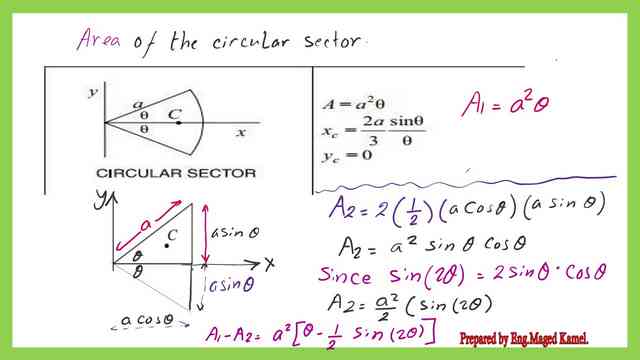
The first area A1 is the area of the circular sector, from the previous post we have estimated it as equal to a^2*θ, where a is the radius and θ is half of the enclosed angle of 2*θ.

The second area A2 is the area of the two triangles, the two areas are equal to 0.5*(2a*sinθ)*a *cosθ=a^2 *sinθ*cosθ.

From trigonometry we have sin(2θ)=2*sinθ*coθ, we can readjust the expression for the area of the two triangles to be equal to a^2*0.5*sin(2θ).

The area of the circular sector can be estimated as A1-A2, which is equal to a^2*(θ-0.5*sin(2θ).

The steps followed to the area for the circular segment are shown in the next slide image.

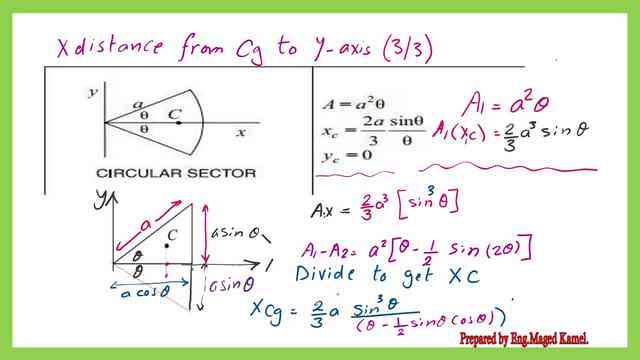
Cg for a circular segment-first moment of area about the Y-axis.

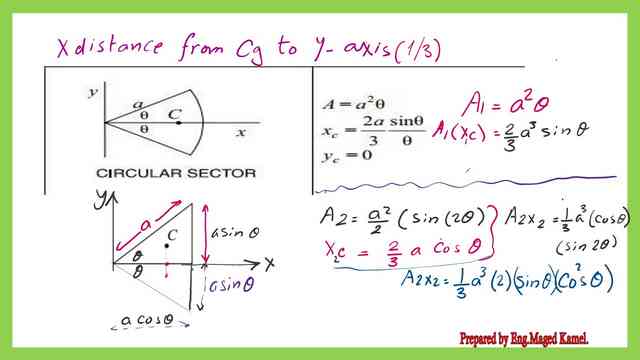
The Cg for a circular segment about Y-axis can be obtained by using the expression (A1*Xcg1-A2*Xcg2)/(A1-A2)

For the first moment of area for a circular sector, we will multiply the area which is a^2*θ by the distance of its Cg to the Y-axis, which is Xcg1, which is equal to (2/3)*a^2*sinθ.

For the first moment of area for the two triangles, we will multiply the area which is 2*0.5*sin(2θ) by the distance of its Cg to the Y-axis, which is Xcg2, which is equal to (2/3)*a*cosθ.

The calculations of the first moment of area for the circular sector and for the two triangles are shown in the next slide.

For more simplification of the expression for the first moment of area for the circular segment about the Y-axis, we will utilize the expression for sin^2θ=1-cos^2θ. The final expression for the first moment of area about the Y-axis is shown in the next slide image.

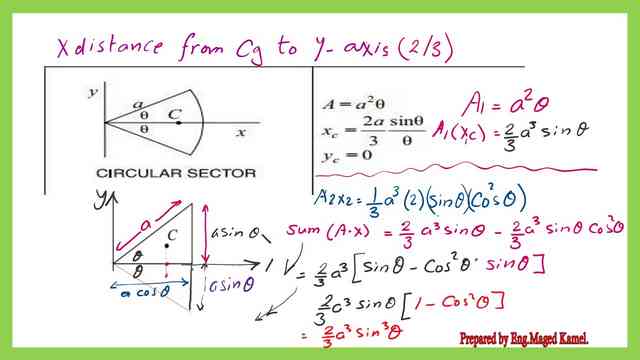
For the expression of Xcg or the distance from Cg of the circular segment, we will divide the first moment of the area by the value of the area of the circular segment. The Xcg is shown in the next slide image.

Cg for a circular segment-first moment of area about the X-axis.

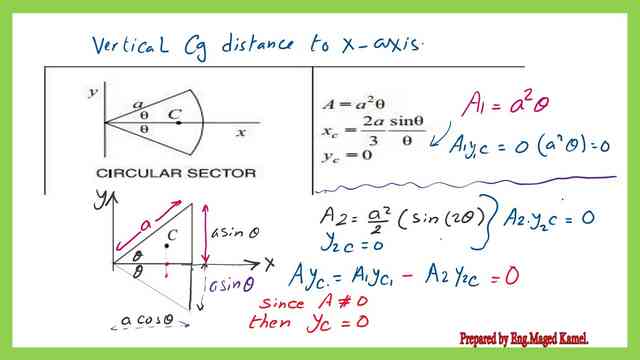
For the area and Cg for a circular segment about X-axis. We can use the expression (A1*Ycg1-A2*Ycg2)/(A1-A2)

For the first moment of area for a circular sector, we will multiply the area which is a^2*θ by the distance of its Cg to the X-axis, which is zero.

For the first moment of area for the two triangles, we will multiply the area which is 2*0.5*sin(2θ) by the distance of its Cg to the Y-axis, which is zero.

The final value of the first moment of area about the x-axis is zero since the area is not equal to zero, this indicates that the Cg is located at the X-axis, and has a zero vertical value.

We have completed the subject of the area and Cg for a circular segment. Thanks a lot.

The next post will be Practice problem 5-8. Find the centroid for the shaded area

This is a link to a very useful site: Engineering Statics open and interactive.