Area and Cg for a semi-circle.
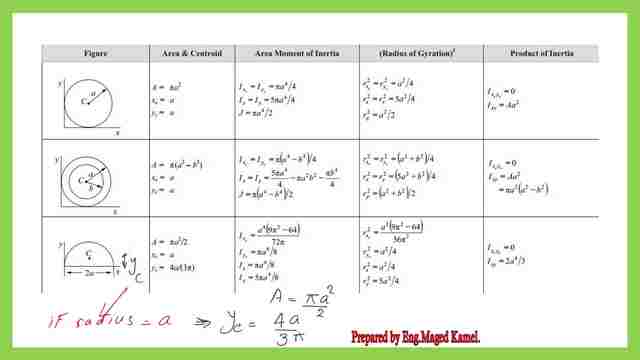
Reference handbook 10.00 value for the area and Cg for a semi-circle.
There is a list of the common round shapes area and CG value. Our third case is the case of a semi-circle.
You can click on any picture to enlarge, then press the small arrow at the right to review all the other images as a slide show.
The external axis Y is tangents to the semi-circle which has a diameter value of 2a. The x-axis is passing by the center of the semi-circle.
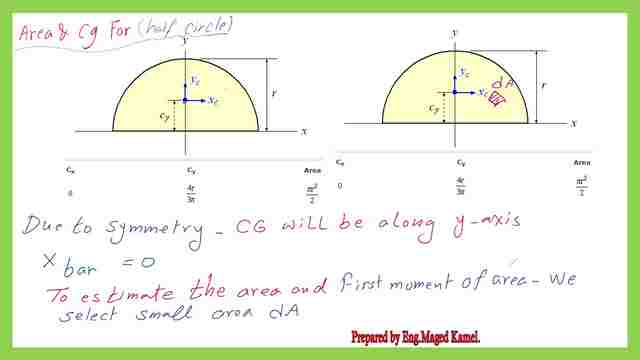
Area and Cg for a semi-circle- select an area dA.
We have a semi-circle with radius a, for which it is required to get the area and CG. We can find that there’s an internal axis Y that divides the semi-circle into two similar parts. Due to that symmetry, we expect that the Cg or the center of gravity will be located along the y axis at a certain distance y from the external axis x. We have used the radius of the semi-circle as equal to r.
We need a small area dA to estimate the first moment of the area and to obtain the value of the total area of the semi-circle.
Area and Cg for a semi-circle-first moment of area about the x-axis.
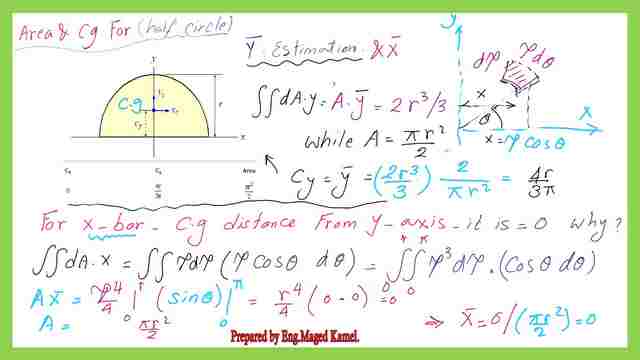
For the area and Cg for a semi-circle about X-axis. We have two intersecting axes X&Y, we will select a small area dA that has a radius of ρ from the intersection of the two axes X and Y.
The first moment of area for the small area dA about the X-axis is the product of that area by the vertical distance to the X-axis. The angle θ is the angle enclosed between the Cg of the strip dA with the X-axis. The angle dθ is the enclosed angle by the strip dA.
The details of the horizontal and vertical distances of the strip dA are shown in the next slide image.
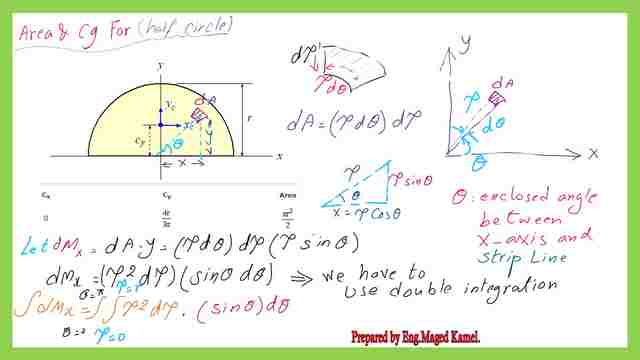
The vertical distance is y which is equal to ρ*sin θ. The moment dMx=dA*(y)=(ρ*dρ*d θ)*(ρ*sin θ). It will be simplified to (ρ^2*dρ*sin θ*dθ).
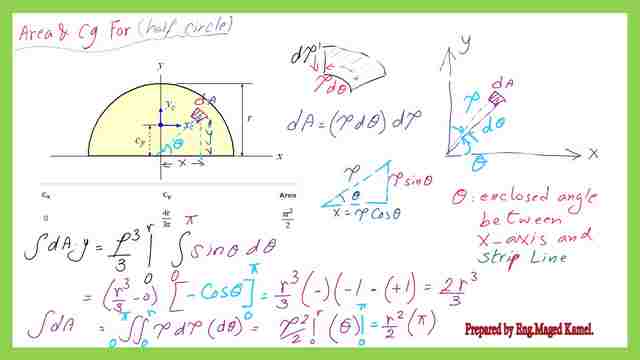
For the first moment of area for the whole semi-circle, we will use double integration since we have to integrate for ρ from ρ=0 to ρ=r. The second integration os for the angle dθ from θ equals to zero to dθ equal to π or 180 degrees. dA*y=∬(ρ^2*dρ*sin θ*dθ).
This is the value of the first integration, ∫ρ^2*dρ from zero to r will be equal to 1/3*ρ^3 after substitution will lead to 1/3*(r^3-0)=r^3/3. While for the second integration ∫(sin θ*dθ)=-cos(θ), after substituting from zero to π. The value will be (- (cos(π)- cos(0))=(-(-1)-(1)=+2. The total value of the first moment of area for the semi-circle will be equal to =2*(r^3/3).
But the semi-circle area can be found from the integration of dA= ∬(ρ*dρ*dθ) from ρ=0 to ρ=a and for dθ from θ equals zero to dθ=π, the final expression for the area is dA=ρ^2*0.5*(θ), substitute to get A=0.50*(r^2-0)*(π-0)=0.50*π*r^2.
The details of the calculations for the first moment of area for the semi-circle about the X-axis and the value of the area are shown in the next slide image.
Divide A*y/A to get Y bar will lead to ybar Cy=2*(r^3/3)/0.5*π*a^2=4a/3*π. This includes that the Cg lies on the X-axis.
Area and Cg for a semi-circle-first moment of area about the Y-axis.
For the area and Cg for a semi-circle about the y-axis. The first moment of area dA about the y’-axis is dMy=dA*(x)=(ρ*dρ*d θ)*(ρ*cos θ). it will be simplified to (ρ^2*dρ*cos θ*dθ).
For the first moment of area for the whole semi-circle, we will use double integration since we have to integrate for ρ from ρ=0 to ρ=r. The second integration os for the angle dθ from θ equals to zero to dθ equal zero to π or 180 degrees. dA*y=∬(ρ^2*dρ*cos θ*dθ).
The value of the first integration is equal to ∫ρ^2*dρ from zero to r=1/3*ρ^3 after substitution will lead to 1/3*(a^3-0)=a^3/3, while the ∫(cos θ*dθ)=-cos(θ), after substitute from zero to π. The value will be (+ (sin(π)-sin(0))=zero.
We have estimated the area of the semi-circle as equal to 0.5*π*r^2 as shown in the next slide image.
The Cg distances are x bar=0 and y bar=4r/3* and are shown in the next slide image.
We have completed the subject of the area and Cg for a semi-circle.
The next post will be on how to estimate the area and Cg for a circular sector.
This is a link to a very useful site: Engineering statics open and interactive.
