Last Updated on June 8, 2024 by Maged kamel

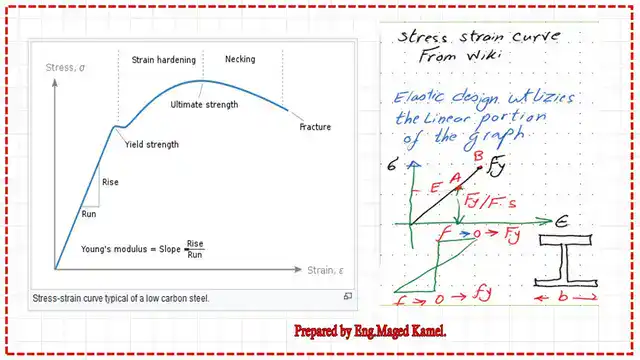
The topics included in our discussion are shown in the next slide. The various regions are shown the relation between stress and strain for mild steel under tension.
The elastic design utilizes the linear portion of the graph, the upper and lower fibers of the section will have f=Fy.

Allowable working stress design method AWSD, quick revision.

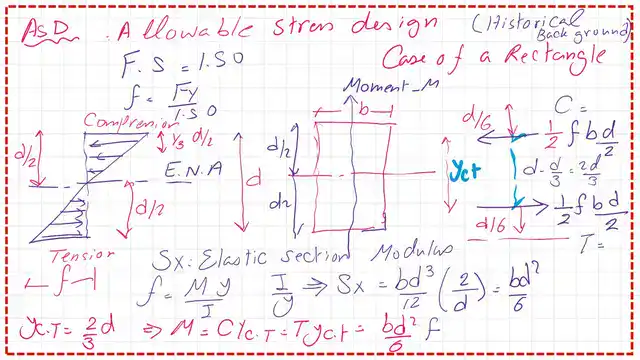
We will start to review the allowable working stress design method in which the compression force acts at a distance of (1/3)*d/2=d/6 from the upper fiber of the section, while the Tension force acts at a distance of d/6 from the lower fiber.

The lever arm of C or T =((d-2*(1/6))=2/3d, which is the distance between the points of application between the compressive force C and the tensile force T and sometimes called Yct is the compression and tension, Yct =2/3d.

The Moment value =f(*b*d^2/6), the value of (b*d^2/6) is called elastic section modulus and denoted by the symbol S. So the moment can be expressed as the product of f*S.

The stress distribution diagram for a section is shown when the design is based on the working stress with a maximum value at the extreme upper fibre=fb. The distribution as shown is linear and the stress value is zero at the neutral axis.

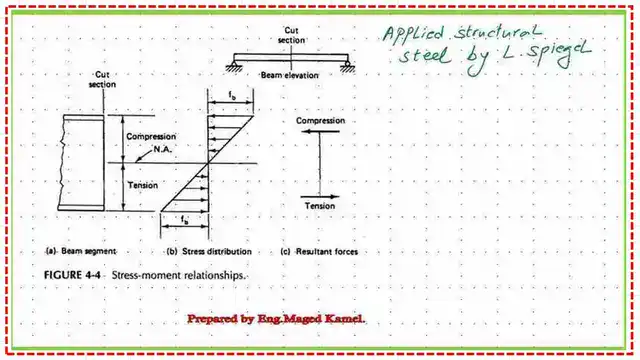
The moment of resistance of the section can be estimated from the value of Fb and the section modulus S, which is the inertia/(h/2) for a rectangular section where h is the overall height of the section.
Again, the moment is MR= Fb*S. The maximum stress value for the compact section was considered to be 0.66Fy.

This is more detail regarding the relationship between Moment and working stress and how to derive the expression.

The triangular stress was converted into two equal forces acting at (2/3 )of (d/2) from the neutral axis, creating a moment equal to the product of T*Yct or c*yct, where yct is the distance between the points of application of C&T forces.

We can derive the final expression by considering the elastic section modulus x as the value of (I/y).

Introduction to the Plastic Theory.

The plastic theory has considered that at the places of maximum moments, the section can be regarded as carrying stresses equal to yield stress, which will lead to a formation of plastic hinges; at these hinges, there will be no ability to take further load, and collapse will develop.

The following assumptions are made:
1-The stress-strain relationship is idealized into two straight lines, as shown in the figure.
2- The plane section before bending remains the plane even after bending.

3-The relationship between compressive stress and compressive strain is the same as between tensile stress and tensile strain.
4-Whenever a moment is attained -at any cross-section, plastic hinge forms, which can undergo rotation of any magnitude, but the bending moment remains constant at the fully plastic value.

5-Effect of axial load and shear on the full moment capacity of the section are neglected.
6-The deflections in structures are small enough for the equations of statical equilibrium to be the same as those for the undeformed structures.

The stain value at the plastic stage/strain at the yield stage is approximately 10. the strain at the stage can be set to 1.50*1/100, as shown in the next picture.

The next slide shows the stages for a rectangular section under applied loads. The elastic stage is where the extreme upper and lower fibers have reached Fy.

Next, under increasing loads, the stresses at the extreme fibers cannot exceed Fy, and then the lower fibers will develop stress equal to Fy, but some fibers have not reached Fy; this stage is called elastic-plastic.
After a further increase in loads, all the rectangular section fibers have been stressed to Fy at the plastic stage. Please refer to the next picture so the section can carry the moment.

This is a link to a good source for steel beams.

This is a link to the next post: Elastic and plastic section moduli?