Last Updated on July 4, 2025 by Maged kamel
The difference between simple and compound interest.
When someone borrows money from the bank and has to repay after some time, in the case of simple interest, as an alternative, if the loan is to be repaid through a compound interest rate, what will be the value?
The difference between simple interest and compound interest is shown. For a simple interest: the final value equals principal(1+% interest)* the number of years.

For compound interest, the final value will be equal to principal*(1+%interest)^(number of years), where the number of years is considered as a power factor.
Example 1.4: How to determine the loan value?
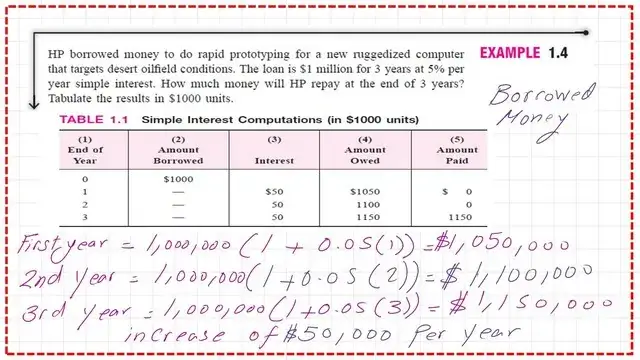
Example 1.4- HP borrowed money to do rapid prototyping for a new ruggedized computer. that targets desert oil field conditions. The loan is $1 million for 3 years at 5% per year simple interest. How much money will HP repay at the end of 3 years?
Solution for Example 1.4. The example is a direct application of simple interest.
HP borrowed money, the loan is $1.0 Million for 3 years at 5% interest as simple interest. How much money will the company repay after the end of the 3 years? The solution is shown in a tabulated form as in the next slide.
Steps to calculate the simple interest value.
1- The borrowed money is $1.00 million.
2-At the end of the first year, simple interest at 5% of the money after one year=$1.0(1+0.05*1.00)=$1.05 million.
3-At the end of the second year, simple interest at 5% of the money after two years =$1.0(1+0.052)=$1.10 Million.
4-At the end of the third year, simple interest at 5% of the money after three years =$1.0(1+0.053)=$1.15 Million.
Money is due at the end of the first year+interest = 1.05+0.052.00=$1.15 million.
Using Excel to get the simple interest value, example 1.4.
For the sake of using practical tools, excel can be used to estimate the future value of the deposit, whether loans, or debts after specifying the interest rate and time, and the principal or the present value at time-0, there is no function for the case of simple interest, but we can create relations between cell.
For the case of our solved example 1.4, our present value is $1.00 million, the simple interest rate is 5% and the period is 3 years. The future values after one year, two years, 5 years, and ten years were estimated, using the formula we used earlier.

Solved problem 1.5 based on compound interest.
Example 1.5 is a direct application of compound interest. HP borrowed money, the loan is $1.0 million for 3 years at 5% interest as compound interest.
How much money will the company repay after the end of the 3 years?
The solution is shown in a tabulated form as in the next slide.
Using Excel for compound interest value, for example-1.5.
For the sake of using practical tools, Excel can be used to estimate the future value of the deposit, whether loans or debts, after specifying the interest rate and time, and the principal or the present value at time (0). There is a function in Excel that is called Fv, or future value.
For the case of our solved example 1.5, our present value is $1.00 million, the compound interest rate is 5% and the period is 3 years. We can put this data in an Excel sheet, as included in the next slide image.

For interest cell is D6 and multiply by 1) to express the future value after one year or, 2 for the case of two years, etc.
This is a comparison between the values estimated by using the simple interest and the
values estimated by the compound interest.

The FV function requires the interest rate, n per, the number of periods, in our case 3 periods, which we are estimating in a yearly rate. It also requires the present value, which is included but with a negative sign.
This is the Excel sheet used to estimate the compound interest values by using the function FV.
As we can see, after the one-year value is =D5 which is the principal value, placed at cell D5, open bracket, inside1+, then another bracket (interest several years))

The next post title is compound interest part 2.
Engineering Economy Applying Theory to Practice is A good referance.