Last Updated on October 27, 2024 by Maged kamel

Column Compressive strength by the general equation.

The content of the lecture is about the Code provision of compression members for global buckling..

I have included some points to be reviewed:

1-The Young modulus of elasticity and Tangent Modulsus of elasticity.

2-Effective length (Kl) for the cases of different end conditions.

3-The Ais provision for Compression members.

4-A solved problem 4.2 for design strength. That problem will be included in a separate post.

The Young modulus of elasticity and Tangent Modulsus of elasticity.

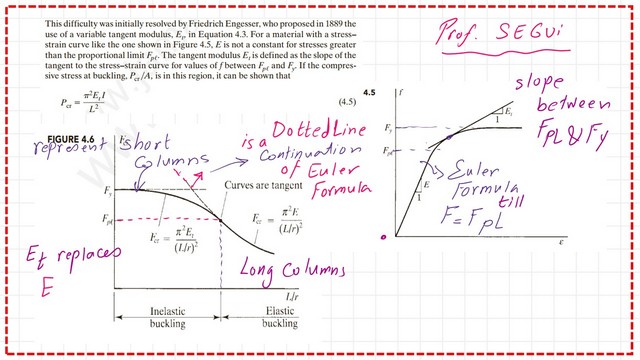
There are two items to consider in evaluating the steel column’s strength: the Young modulus of elasticity and the Tangent modulus of elasticity. For long columns, the Young modulus of elasticity is used to evaluate the critical stress passed on the Euler formula. The Euler formula gives an exact result until a critical stress value of proportional limit stress Fpt holds good.

Another item is that the tangent modulus of elasticity was introduced to find the critical stresses for the short and intermediate columns. That tangent is taken to graph between strain and stress diagram at a stress value between Fcr and Fy.

If a graph is drawn between the slenderness ratio and stress, we can find that the graph consists of two parts. The right part represents the elastic buckling for columns where the stress values for the long column till(K*L/r) equals 4.71*sqrt(E/Fy).

The left side represents inelastic buckling, which includes the stress values for short and intermediate columns where Fcr=Pi2*Et/(Kl) 2. The dotted line represents the Euler graph of critical stress, which gives higher values.

The effect length Kl with different end conditions.

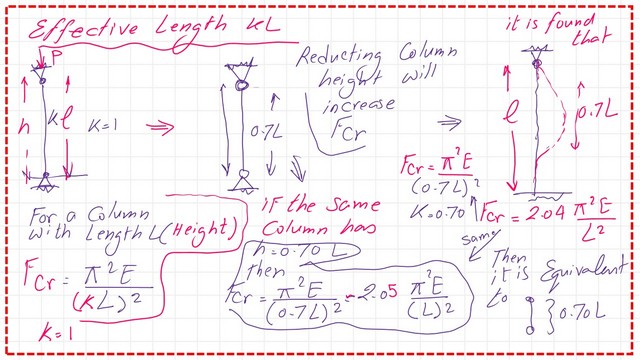
We will be reviewing the effective length Kl for columns. If we have a hinged column at the ends acted upon by a compressive load, the critical stress can be represented by Fcr=Pi2*E/(Kl) 2 . For the same column but with a height of 0.70L, the critical stress will be increased, and it will equal 2.05*Pi2*E/(Kl) 2, which is more than the double value for a column with length l.

The same critical stress value can be obtained for a column with a height L of but fixed at one side and hinged on the other side, so to use the Euler Fcr expression, the denominator is equal to (0.70L)^2, that column is identical to a column with an effective length Kl=0.7L, and the derived K value equals to 0.70.

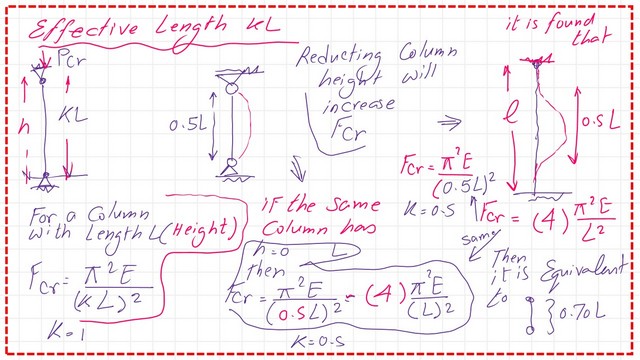
If a compressive load acts upon a hinged column at the ends, the critical stress can be represented by Fcr=Pi2*E/(Kl) 2. The critical stress will be increased for the same column but with a height of 0.50 L, equaling 4*Pi2*E/(Kl) 2.

The same critical stress value can be obtained for a column with a height L of but fixed at both sides, so to use the Euler Fcr expression, the denominator is equal to (0.50L)^2, that column is identical to a column with an effective length Kl=0.5L, and the derived K value equals to 0.50.

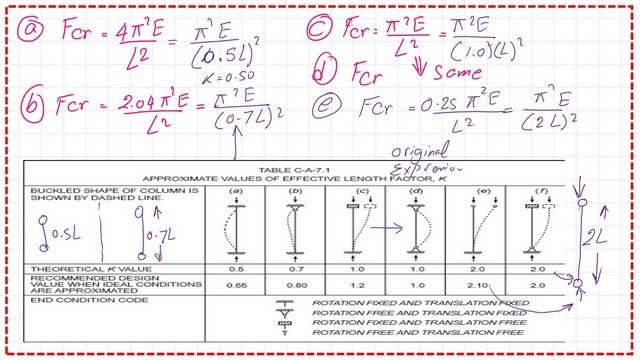
Please refer to the following table for effective length values for the different end conditions and the corresponding Fcr values.

Introduction to the General Provision.

As of today, our subject will be the American code provision of compression members to get the value of the column compressive strength and also solve the problem of separating short and long columns; there is a graph based on the AISC code.

The Aisc chapter for compression members.

Chapter E is the AISC chapter containing the different provisions for compression members for CM#14 and AISC-360-10, on page 16.1-31, and for CM#15 and AISC-360-16, on page “16.1-33”.

The horizontal axis x resembles the quantity KL/r, which becomes Lc/r in the recent codes, the slenderness ratio, and for the y-axis, the division of Fcr /Fy, where Fcr is the critical load /area, which is the compressive strength.

The Aisc has considered the critical stress as reduced Euler stress, which equals 0.877*FE for Long columns. Instead of using the formula Fcr=Pi2*Et/(Kl) 2 for short and intermediate columns, the used formula is (0.658 ^ (Fy/Fe) * Fy, where Fy is the yield stress. and FE is the Euler stress.   

The value for KL/r, which differentiates between long and short columns, is set to 4.71* sqrt( E/Fy).
If the kL/r value is greater than the previous value, then the column is considered a long column, and 0.877 Fe represents the equation. But if the kl/r value is <  4.71 *sqrt( E/Fy), then the column is considered as a short column. The parameters for LRFD the Φ =0.90),  while the Ω for  ASD=1.67, in the old books the Φ was =0.85.  The next slide image shows the data.      
                                                 

The next slide shows the difference between E2 provision. in Aisc-360-2010 and the similar E2 provision In AISC-360-16, where Kl/r was replaced by Lc/r.

  Flexural buckling of members without slender elements.

For the local buckling,  here again, we review the effective length symbols as L=laterally unbraced length of the member, r is the radius of gyration, k is the value for the end conditions of the column.  The chapter which is relating to the columns in the code is chapter  E, while chapter F is for bending moments for beams is chapter F.

For the equation E3-1, the  Pn, where Pn is the nominal load Pn = Fcr * Ag. As previously mentioned, if (k*L/r) < 4.*sqrt( E/Fy), then, column compressive strength fcr is estimated from the formula = 0.658 ^(Fy/Fe) all *Fy, and the column is short. But if (k*L/r) > 4.71 * the Sqrt( E/Fy), then the column is long.

The next slide image shows the E3.1-E3-63 in the Aisc-360-16 specifications.

Fe is the buckling stress determined by using equation E3-4 from AISC, and next is the difference in the expressions between AISC-360-10 and 16.

The next post is Solved problem 4-2-how to find design compressive strength?

For a good reference from Prof. T. Bart Quimby, P.E, Ph.D., F.ASCE, refer to this link for Limit State of Flexural Buckling for Compact and Non-compact Sections.