Last Updated on March 9, 2026 by Maged kamel
Two Solved Problems For Economic Equivalence.
A solved problem for Economic Equivalence.
Problem 1.3 is solved in Prof. Anthony Tarquin’s book, Basics of Engineering Economy.
The following solved problem on Economic Equivalence is a good example of Equivalence, as the five different statements need to be checked to determine whether they are correct.
Problem 1.3- AC-Delco makes auto batteries available to General Motors dealers through a privately owned distributorship.
In general, batteries are stored throughout the year.
A 5% cost increase is added each year to cover the distributorship owner’s inventory carrying charges. Assume you own the City Center Delco facility.
Make the calculations necessary to show which of the following statements are true and which are false about battery costs.
a. The amount of $98 now is equivalent to a cost of $105.60 one year from now.
b. A truck battery that cost $200 one year ago is now equivalent to $205.
c. A $38 cost now is equivalent to $39.90 one year from now.
d. A $ 3,000 cost now is equivalent to $ 2,887.14 one year ago.
e. The carrying charge accumulated in 1 year on an investment of $2000 worth of batteries is $100.
The solution for the solved problem of Economic equivalence for all the different statements is as follows:
1-The first option for economic equivalence of $98 to $105.60 with a rate of 5 % is a false statement since 98*(1.05)=$102.90, which is the value after one year, does not equal $105.60.
2. The second option for the equivalence of $200 of truck battery cost one year ago is not equivalent to $ 205.00 now, with a rate of 5%. The statement is false since 200*(1.05)=$210 does not equal $205.0.
3- The third option for the equivalence of $38 cost now is not equivalent to $39.90 one year from now, with a rate of 5 %. The statement is false, since 38*(1.05)=$39.90.
4- The fourth option for the equivalence of a $3000 cost now is not equivalent to a $2887.14 cost one year ago, with a rate of 5 %. The statement is false since 3000/(1.05)=$2857.14 does not equal $2887.14.
5-The fifth option for the equivalence of $2000, carrying a charge of $100, with a rate of 5%. The statement is truesince 2000*0.05=$100.
Economic equivalence is a crucial principle for comparing alternatives.
The second of the two solved problems on economic equivalence.
If we have several alternatives, the method of comparison involves choosing a time period and determining the present value of the flows.
A solved problem is quoted from Contemporary Engineering Economics 6th Edition by Chan Park (Author). It is not included in the video.
Let us suppose that an electronics manufacturing company buys a machine for $25,000 and borrows $20,000 from a bank at an annual interest rate of 9%. Additionally, the company charges a $200 loan origination fee when the loan is initiated.
The bank offers two plans as follows: plan 1– P=$20,000 with interest is 9% plus a $200 fee at the first year and in equal installments of $5141.85 from year 1 to year 5 with a total number of five.
The second plan, Plan 2, involves paying a $200 loan fee at time=0 and making equal installments of $1,800, with 4 payments starting at time t=1 and concluding with the final payment at time t=5. Both plans have the exact 5-year timetable and a 9% yearly interest rate.
Table 3.1 shows the details of each plan.
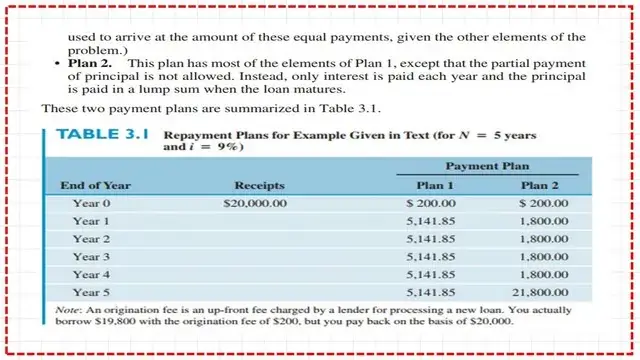
How could we compare the two plans? Is the comparison based on the total amount of payments?
For instance, for Plan One, the total payment amount will be $200 + $ 5,141.85 × 5 = $25,909. For Plan Two, the total payment amount will be $200 + $1800 × 4 + $21,800 = $29,200.
The criteria for comparison between the two plans are based on economic equivalence. Both plans have the same five-year term and 9% interest rate.
By converting each payment into its future value at time 5, and comparing these future values of the two plans, we can then select the appropriate plan. Here is the cash flow diagram for both plans.
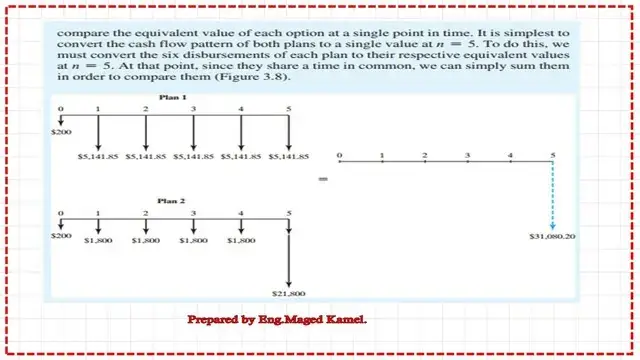
Detailed calculations of plan 1.
This is the detailed calculation for plan-1: pay $200 at time=0, and equal installments of $5,141.85; the total number of payments is 5, starting from time t=1. We sum all future values of these payments. We get $31,080.
Detailed calculations of plan 2.
These are the detailed calculations for plan 2: pay $200 at time=0, and equal installments of $1,800. The total numbers are 5, starting from time t=1. We sum all future values of these payments. We get $31,080.
This is the complete calculation for plan 2. Comparing the future worth value of both plans, we will find that they have the same F5 value and future value at the end of the fifth year. Hence, these plans are economically equivalent.
The borrower can then select the plan that best suits them.
The PDF used to illustrate this post can be downloaded from the following document.
The following post title is “Simple Interest and Compound Interest Part -1″.
Engineering Economy: Applying Theory to Practice is a good reference.