Last Updated on May 30, 2025 by Maged kamel
Introduction to Buckling for columns-part 2.
A first Solved problem for critical load value.
To decide which will control the buckling, we need to estimate the value of(KL/r) on both the major and minor axes and select the highest value between these two values.
The higher value of (Kl/r) will control the buckling, implying estimating stresses for comparison. If we deal with the load, we will select the higher(Kl) value. The numerator has a value of π^2 EI for each axis.
The following item is the first solved problem for the major and minor axes, which will guide us in estimating the controlling compressive load.
Estimating the buckling strength for a column with different end conditions for both the major and minor axes is required.
Determine the buckling strength for the given steel shape W2x50, which is pinned at both ends and has a column height of 20 ft high for the minor axis.

The above slide image shows the minor axis bent from both ends on the right side. For the major axis, Buckling is fixed on one end and pinned on the left side.
We solve this problem by using Euler’s formula for the critical load estimated as Pcr=π^2 EI/(KL)^2. Since this is a W section, we need to use Table 1-1, pages 1-26, to get the inertia value Ix for the major- axis and Iy for the inertia value for the minor axis. For the major axis direction, E = 29*10^6 psi, we have Ix = 391 in^4, k value = 0.70.
Since it is fixed-pinned, we will use k = 0.80, as recommended by the code. We will substitute for x-direction the critical load is Pcr at x =π^2 EI/(KL)x^2=π^2*(29*10^6)*391/(0.8*20*12)^2*1/1000= 3035.80 kips.

We have Iy=56.30 inch4, k=1.00 for the minor direction since the column is pinned-pinned.
For the critical load in the y-direction, Pcr at y =π^2 EI/(KL)y^2=π^2*29*10^6)*56.30/(0.8*20*12)^2*1/1000= 280 kips. We will select the smaller value of 280.53 kips. The minor axis governs the buckling.

Check whether yielding occurs before buckling.
For the previous problem, to Check whether yielding occurs before buckling, we estimate the compression stress. We have Pcr = 280 kips, while the area of the W section equals 14.60. The stress equals P/A=280/14.60=19.17 ksi, which is less than the yield stress of 50 ksi, which indicates that buckling occurs before yielding.
Case 2: yielding occurs before buckling.
If the previous column height is reduced to 10 feet, the critical load is equal to 1119.94 kips; the stress will be equal to 1119.94/14.60=76.70 ksi, which is bigger than 50 ksi, the yield stress, in this case, yielding occurs before buckling.

Please refer to Professor Varma’s notes in the next slide image.

A second Solved problem for the major and minor axis.
We will modify the end conditions for the column, which was included in the first solved problem while keeping the column’s height equal to 20 feet. The column in the major direction—x is pinned at both ends. The column in the Y direction is pinned at one end and fixed at the other end.
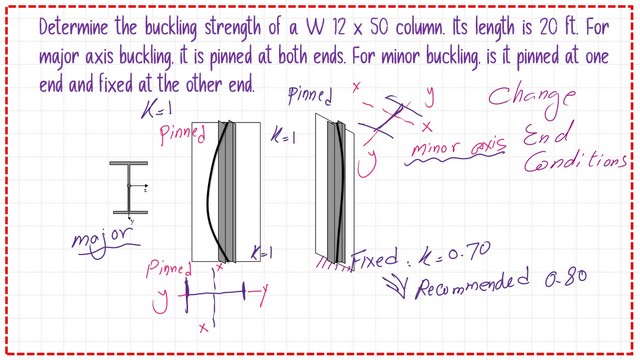
the critical load is Pcr at x =π^2 EI/(KL)x^2=π^2*(29*10^6)*391/(20*12)^2*1/1000= 1942.9 kips.

Please refer to the next slide image for the estimate of the critical load for the column at the y- y-y-direction. The final Pcr value is 437.12 kips in the y-direction. This load is chosen since it is less than Pcr at x, which equals 1942.90 kips.

The next slide shows the different types of bracing for frames. There are X and K braces, and bracing can be done using shear walls.

The difference between the braced and unbraced frames. Due to bracing, the frame will have slight or no lateral movement.

The next post: Column compressive strength by the general equation.
For a good reference from Prof. T. Bart Quimby, P.E., Ph.D., F.ASCE, refer to this link for public concepts.