Last Updated on April 3, 2024 by Maged kamel
Column Compressive strength by the general equation.
The content of the lecture is about the Code provision of compression members for global buckling..

Introduction to the General Provision.
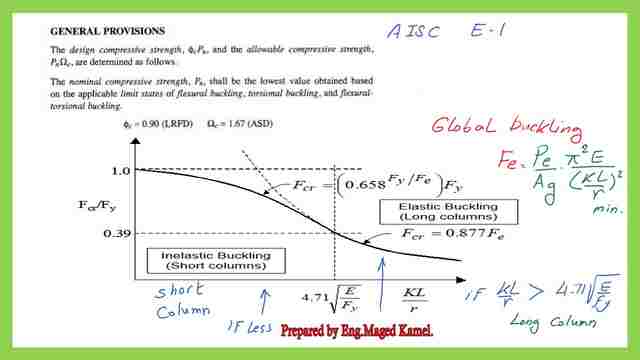
Our subject as of today will be the American code provision of compression members, to get the value of the column compressive strength and also a solved problem to differentiate between short and long columns, there is a graph based on the AISC code. The horizontal axis x resembles the quantity KL/r, the slenderness ratio, and for the y-axis the division of Fcr /Fy, where Fcr is the critical load /area, which is the compressive strength.
The curve consists of two shapes, the one at the left is the equation of short columns, and inelastic buckling, while the curve at the right is the equation of Euler for long columns and the dotted line is the extension of the Euler equation.
At the right side of the vertical dotted line is the equation of Euler for long columns, elastic buckling, which is for long columns represented by the equation Fcr=0.877Fe, Where Fe is the item =(Pe/Ag), for which Pe /ag= π^2 E/(KL/r)^2, that is what the AISC has established the equation for the critical load estimation.
For the other equation, the column compressive strength is estimated as (0.658 ^ (Fy/Fe) * Fy, where Fy is the yield stress.
The other curve at the left side gives the value of 1 at the intersection with the y-axis, the value for KL/r, which differentiates between long and short columns is set = 4.71* sqrt( E/Fy).
If the kL/r value is greater than the previous value, then the column is considered a long column, and the equation is represented by 0.877 Fe. But if the kl/r value is < 4.71 *sqrt( E/Fy), then the column is considered as a short column, the Fcr is given by the equation column compressive strength Fcr =( 0.658 ^ Fy/Fe * Fy), the parameters for LRFD the Φ =0.90), while the Ω for ASD=1.67, in the old books the Φ was =0.85.
The next slide shows the symbols used for the effective length factor and the AISC provision.

Flexural buckling of members without slender elements.
For the local buckling, here again, we review the effective length symbols as L=laterally unbraced length of the member, r is the radius of gyration, k is the value for the end conditions of the column. The chapter which is relating to the columns in the code is chapter E, while chapter F is for bending moments for beams is chapter F.
For the equation E3-1, the Pn, where Pn is the nominal load Pn = Fcr * Ag. As previously mentioned, if (k*L/r) < 4.*sqrt( E/Fy), then, column compressive strength fcr is estimated from the formula = 0.658 ^(Fy/Fe) all *Fy, and the column is short.But if (k*L/r) > 4.71 * the Sqrt( E/Fy), then the column is long.

Fe is the buckling stress determined by using equation E3-4 from AISC.

This is the pdf file used in the illustration of this post and the next post.
The next post is Solved problem 4-20-how to find design compressive strength?
For a good reference from Prof. T. Bart Quimby, P.E, Ph.D., F.ASCE, refer to this link for Limit State of Flexural Buckling for Compact and Non-compact Sections.

