Last Updated on June 7, 2024 by Maged kamel

Part 4/4 of the Solved Problem 9-9-6, How To Find LL? 

How to estimate the Cb for the beam-Part 4/4 of the Solved Problem 9-9-6.

Cb for a simply supported beam under uniformly distributed, this is included in part 4/4 of the Solved Problem 9-9-6. This is a reminder of the Cb value for parts AB and CD.

We have one roller support at one end and a hinged one at the other. The bracing spacing is every L/3 distance, where L is the span length. We will take the first part of L/3 and magnify it. This is part BC.
The reaction for the beam at the left hinge = W*L/2=Reaction at the right support.

We need to estimate the moment values at B’, B”, C’, and C. The L/3 length is to be divided into four sections. So we have L/12 intervals between these points. Then, we can estimate the CB equation. CB=(12.50*M-max)/(2.50 M-max+3*Mb’+4*MB”+3*Mc’)

The next slide image shows the different values for the moment at the four points.

From the next slide. Use the equation of CB=(12.50*M-max)/(2.50 M-max+3*Ma+4*Mb+3*Mc).

The value of Cb=12.50/8*(234+210)/288=1.01, the beam has three values of Cb as (1.46,1.01,1.46), the CB can be used to increase the Mn.

How to estimate the Mn for the beam?

The next step is to estimate the Mn value based on the limit state of the lateral-torsional buckling.

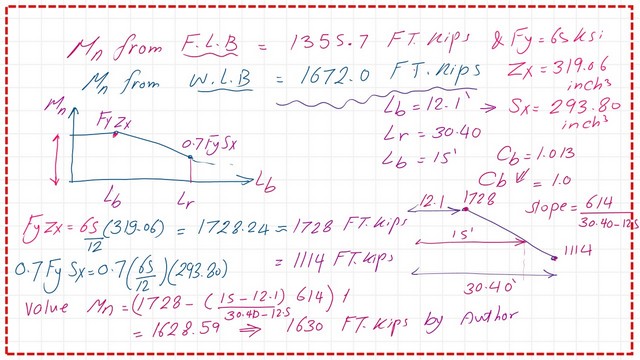
We have Lp =12.10′ while Lr = 30.41′, and the actual bracing length is 15′, as given in the solved problem. We have Mp=1728 at Lb=12.10 and Mr=0.70*Fy*Sx=1114 at Lb=Lr.

At the 15′ distance Mn=Cb* (1728-1728* (1728-1114)/(30.41-12.10)*(15-12.10), if we so we can use cb as=1.01, taken as =1.0 by prof. Salmon.

The next slide shows a graph of Lb and Mn values—at Lp=12′, Mn=1728 ft, while for Lr=30.41′, Mn=1114 ft. kips.

The Mn value for cb=1.00 will equal 1630 ft. kips for lateral torsional buckling. The slide shows the three values. This is a reminder about the Mn in the case of local flange buckling.

This is a reminder of the Mn from the flange and web local buckling case.

We have three Mn values: one from the local buckling of the flange, which is equal to 1355.7 ft-kips; the second from the local buckling of the web, which is 1672 Ft-kips; and the third, 1630 ft. kips.

The minimum selected value of Mn is 1355.70 ft-kips.
The LRFD value multiplied by φb will be φb*Mn=0.90*1355.70=1220 ft-kips.

How can the LL for the beam- part 4/4 of the Solved problem 9-9-6 be estimated?

The ultimate load for the simple beam Mult must be =< 1220 ft.kips.
From the next slide, the Dead load included the own weight=(0.15*1.2+1.60*LL)*(45^2)/8<=1220 ft-kips. Then (0.18+1.60*LL)*253.125<=1220.  1.60*LL=(1220/253.125)-0.18=4.639. LL=4.639/1.60=2.899 Kips/ft. Taken as LL=2.90 kip/ft, which matches the final solution by Prof. Salmon. Thanks a lot.

This is the next post,  Moment Redistribution For Continuous Steel Beams. The post introduces the method for moment redistribution, setting the AISc code to reduce negative moments and adding 0.10 to the average value between supports and positive moments.

For useful external resources for steel beams. Chapter 8 – Bending Members