Last Updated on June 14, 2025 by Maged kamel
We will introduce two practice problems for Ixy for trapezium, 8.43 and 8.49. These problems are quoted from BEDFORD’s Engineering mechanics statics.
Two Practice problems for Ixy for trapezium.
The first practice problem for inertia is 8.43. Find Ixy for a given trapezium.
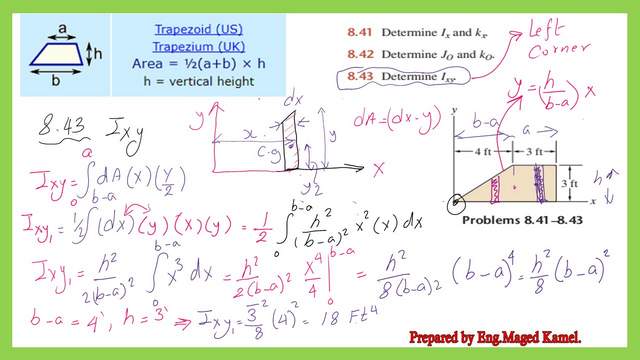
For the first of the two Practice problems for polar Ixy for trapezium, we have a trapezium with a base length of 7 feet, an upper part length of 3 feet, and a height of 3 feet. It is required to determine the product of inertia Ixy.
We will start to estimate Ixy in two parts. The first part is Ixy1, or the product of inertia for the triangular portion about the point of intersection of the two axes X and y. We call it Ixy1. For a small strip dA, the value of this area is dx*y. The area dA creates dIxy about the point of intersection of axes X and y.
The product of inertia dIxy1=(dA*x*y/2)=(x*y^2*1/2*dx), but y has a relation of x as y=(h/(b-a)*x ,so the dIxy1can be rewritten as (h^2/(2*(b-a)^2)*(x^3*dx). We will integrate from 0 to (b-a) for the triangular portion.
finally the expression for Ixy1 can be written as (h^2*(b-a)^2/8). We can substitute for the values of h, a, and b for h value it is equal to 3Ft and for a it is equal to 3feet and b equals 7 feet, we can substitute these values in the Ixy1 expression. The Ixy1 value is equal to 18Ft4. Please refer to the next slide image for more details.
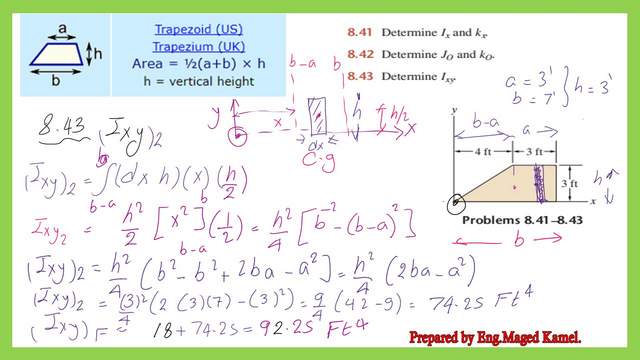
Ixy2 for a given trapezium by integration using a vertical strip.
The next step is to get the Ixy2 value for the rectangular portion, the dIxy2 equals (dx*h^2*x/2), we will integrate from b-a to b, and the final value of Ixy2 can be found as equal to 74.25 Ft4. The final product of inertia Ixy for the given Trapezium will be equal to 92.25 Ft4.
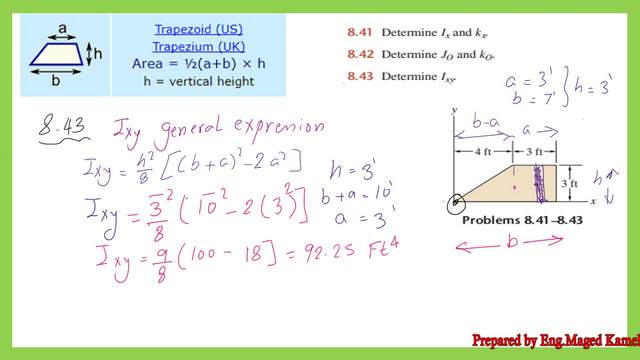
Derive a general expression for Ixy for trapezium.
To derive an expression for Ixy, we add the two values Ixy1 and Ixy2; there are common items that we can simplify. for a more detailed illustration please refer to the next slide image, the final Ixy expression is shown.
We can substitute the values of b, a, and h, and then we can obtain the final value of Ixy as equal to 92.25 ft^4, which is the same value we obtained earlier. For more details, please refer to the next slide image.
The second practice problem for inertia is 8.48. Find Ixy for a given trapezium about the Cg.
For the second practice problem 8.48 of the two practice problems for Ixy for trapezium, it is required to find the Ixy value for the trapezium at the Cg.
We have obtained the values of x̄ and ȳ from the previous posts, and the area of the trapezium is 15 ft². The product of inertia about the Cg is equal to Ixy minus the product of area by (xbar*ybar). The final value of Ixy at the Cg is 7.10 ft4.
We ended after solving the two Practice problems for Ixy for trapezium.
Thank you very much, and I look forward to seeing you in the next post.
Please refer to post 19 for more information about Ix for a trapezium.
Please refer to post 22 for more information about Iy for a trapezium.
The previous post, Post 26-Two: Practice Problems for the Polar Inertia of a Trapezium.
A useful external resource for the area, Cg, and inertia for the parallelogram, please refer to this link.
A new subject for maximum and minimum moment of inertia will be followed. Please refer to post 1; Easy illustration of the theory of pure bending.