Last Updated on September 15, 2026 by Maged kamel
Solved problem 5-1- part 2.
Solved problem-5-1-part 2. is the title of this Post, in which we continue solving problem 5.1; we have obtained the required Value of the Moment of Inertia, Ix, as equal to 440 inch4. We have selected W14x30 based on a Zx Value of 44.40 inch3; we need to check its Ix Value from Table 1-1. The Ix Value is 291.0 in4, which is smaller than 440.0 in4. So, we need to revise the selection.
This is a reminder of the Moment of Inertia of the required W section based on Deflection due to live Load, where we have used the factor C1 as equal to 161, and the total Moment Value Mt and the square Value of the length of the steel Beam.
This is a reminder of the Moment of Inertia of the required W section based on Deflection due to the toL and the square Value of the length of the steel Beam.
Use Table 3-3 to select a new W section with Ix>or equal to the required Value by Deflection criteria, which is 440 inch4.
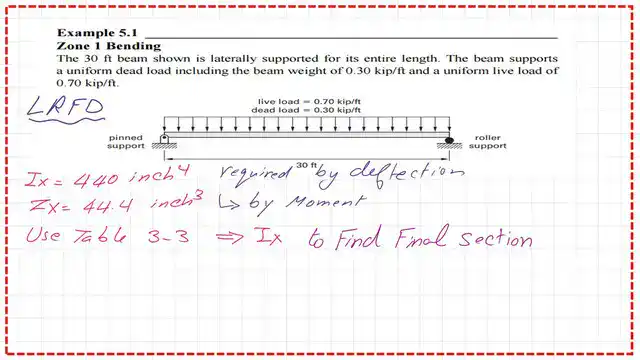
Use Table 3-3 for the solved problem 5-1-LRFD design.
Use Table 3-3 to select a new W and use the bold W18x35. Table 3-3 gives a section Ix of 510 in^4, greater than 440 in^4.
We have selected the first four W sections with Ix greater than 440 inch4. We need to get the Zx values for these sections and select the final W section.
The next slide images show the data for the four sections and why we have selected W18x35.
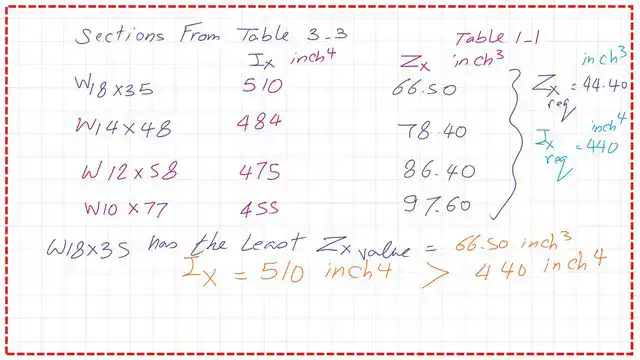
We will estimate the design strength for W18x35 using LRFD. It will be equal 249 ft. kips, which is greater than the Ultimate Moment of 166.50 ft-kips. Kips. Section W18x35 is adequate for design since the available strength exceeds the ultimate Moment.
Find the required Zx based on the ASD design.
We need to estimate the required plastic section Modulus Zx for the Beam based on the ASD design. The total Moment based on the given data equals 112.50 ft·kips, and the required Zx equals 45.09 in3; the necessary calculation is shown in the next slide image.
Based on the Inertia requirement from the Deflection control estimate, the required Inertia Ix is 440 in4 and the required plastic section Modulus Zx is 45.09 in3; use Table 3-3 based on Ix to find the proper section.
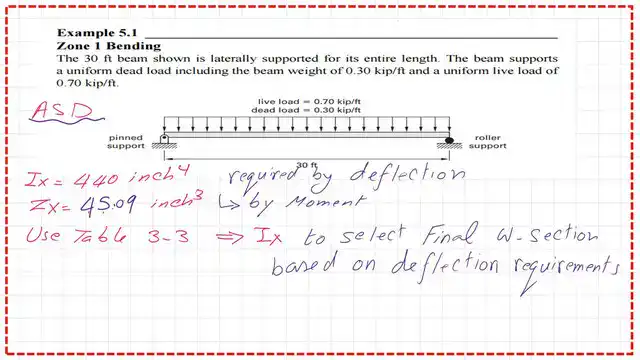
Use Table 3-3 for the solved problem-5-1-ASD design.
Use Table 3-3 to select a new W section and use the bold W18x35. This gives a moment of Inertia Ix of 510 in4, which is greater than the required Moment of Inertia of 440 in4.
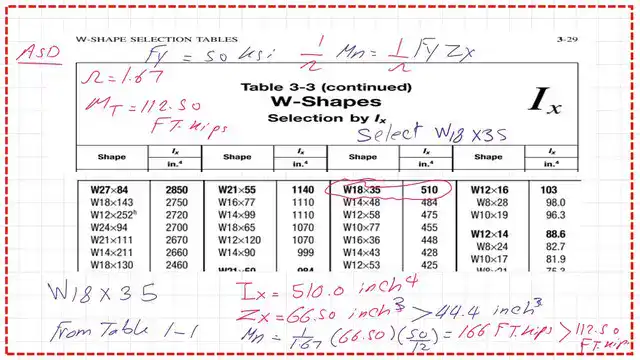
The total Moment for the ASD design is 112.50 ft-kips. The allowable strength for W18x35 is (1/omega)*Mt/Zx*Fy, estimated at 166.0 ft-kips. This Value is bigger than the Total Moment. The section is adequate for ASD design. Please refer to the following slide image for more information. Thanks a lot.
Test your understanding
This is a new Quiz to check your understanding. There are two questions. Please sign in to get verification of your answer via email.
#1. For the Given problem 5-1, if we change the dead load Wd to 0.70 K/Ft. Select the required Ix value by total load and by Live load only. ? Ix required by total Load and live load.
Select all that apply:
#2. What is the selected W section based on deflection requirements? Choose from the following options.
You can view or download the PDF for this Post from the following document.
As an external resource for Deflectiontion. Chapter 8 – Bending Members- 14th edition.
External resource for Deflectiontion. Chapter 8 – Bending Members-15th edition.
As an external resource for Deflectiontion. Chapter 8 – Bending Members-16th edition.
For the Post , 25-part-1-4-solved-problem-9-9-6: How to find LL for a given slender section?