Last Updated on October 10, 2024 by Maged kamel

Part 1/4 of the solved Problem 9-9-6, How To Find Service LL?

Solved problem 9.9.6 From Prof. Salmon’s Book.

This is the content of the lecture and the sequence of items for calculations of the solved problem 9-9-6.

A solved problem 9.9.6 from Prof. Charles Salmon’s book. A solved problem 9.9.6 from Prof. Charles Salmon’s book.
Please look at the small sketch, given the welded I-beam section used as a 45-ft beam laterally supported at the one-third point.

The I-beam section consists of three plates welded together; the Upper plate representing the flange is a plate with the dimension of  (16″x5/8″).

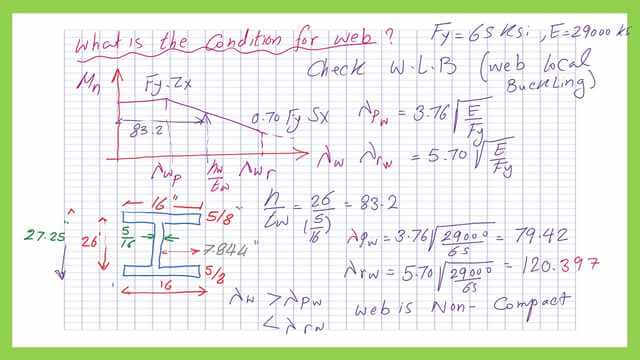
The web part is a plate with a dimension of  (26″x5/16″).

The lower flange plate is similar to the upper plate (16″x5/8″), the yield stress Fy is given as 65 ksi, E the modulus of elasticity is  29×10^6 psi or sometimes written as 29000 ksi. Loadings are shown in the next image; bracings are located at the third point.

We want to check the compactness of the flange and web and find out what F equation we will use. Please refer to the details of the different F types for doubly symmetric sections based on Chapter F of the specification.

What is the local buckling λ parameter for the flange?

We cannot take λr=1*sqrt(E/Fy) as case no.1  for flanges of Rolled I-shaped sections. We will use case No .11 to get the values for λp and λr for the flange of the Built-up section. Please refer to case Number 15 of Table B4.1b for the web parameters.

This is a clear copy of Case 11 for the Built-up section, where the Flange λp has the same value as the first case, λp=0.38*sqrt(E/Fy), while λr=0.95*sqrt(Kc*E/Fy), which has a new factor called Kc.

This is a clear copy of Case 15 for the Built-up section, where, For the web, λp=3.76*sqrt(E/Fy), while  λr=5.70*sqrt(Kc*E/Fy).

This is the calculation for the coefficient of the Kc value. This is the Built-up section,16″x5/8″, and the inner height is 26″ with thickness =5/16″. kc factor=4/sqrt(h/tw), h/tw=26/(5/16)=83.20,then kc=4/sqrt(83.20)=0.4385. kc should be >0.35 but < 0.763; in our case, we have 0.4385.

Find λp and λr for the Flange Local buckling parameters.

The Built-Up section is given, and we have λp for the flange equal to 0.38*sqrt(E/Fy). Since E=29000 psi and Fy=65 ksi, the value of λrF will equal 8.026.
While for flange, we have λr, which is equal to 0.95*sqrt(Kc*E/Fy). Since E=29000 psi and Fy=65 ksi. t value of λrF will be equal to 0.950.95*sqrt(Kc*E/Fl)= 0.95 *sqrt(0.44*29000/0.7*65)=15.90.

Bf/2Tf =16/2*5/8=12.80. The Value of Bf/2tf is bigger than λp but less than λr. Thus, the flange is Non-compact. The Mn will be less than Fy*Zx and bigger than 0.75Fy*Sx.

Estimation of Zx for the section for the solved problem 9-9-6.

What is the value of Mp and also the value of 0.70*Fy*Sx? We must estimate the Zx and Sx values for the solved problem 9-9-6. What is the formula for Zx?

This is the total section due to bending. A compression force will act on the CG of half of the section. The neutral axis N -A is in the middle, but the force, there are two forces, C1 and C2. C2 acts on the web side until the N-A. C1 and C2 have equivalent forces to T1 and T2. These forces develop the plastic moment Mp.

Zx=At*(2*y bar)/2,  2*y-bar is the distance between the Cg of Compression force and Tension force. We call it Yct, or the distance between compression and tension forces.
The plastic section modulus Zx=At*Y bar. The formula is widely used for irregular shapes.

AT/2 is the area of the top flange and half area of the web AT/2=A1+A2.
AT/2=(16*5/8)+(13*5/16))=10+4.06=14.06 inch2. Y1 is the distance from CG of the first area A1 to the N A.
Y1=13+0.50*(5/8)=13+(5/16)=13.3125″.

For A2, the height=13″ and thickness=5/16, then Y2=13/2″. AT/2*Y bar=A1*y1+A2*y2, then ybar=10*13.3125+4.06*6.50)/14.062. ybar=11.344″.

Zx=At*y bar=2*(14.06)*11.344=319.06 inch3. For the upper point of the graph, Mp=Fy*Zx.

Find λp and λr for the Flange Local buckling parameters.

For the web the h is=26′, tw=5/16″, λw=26/(5/16)=83.20. λwp=3.76*sqrt(E/fy)= 3.76*sqrt(29000/65)=79.46.
λw is >λwp.

 Let us check the value of λw-r= 5.7*sqrt(E/Fy)=5.7*sqrt(29000/65)=120.40, λw is >λwp. but <λwr, the section is also non-compact for the web for the local buckling.

The section is non-compact for both the flange and the web due to λ values >λp. but <λr Mn will be < Mp.
Mn is not the product of Fy*ZX. This is the end of part 1 for solving problem 9-9-6.

For the next post, part 2/4 of the Solved problem 9-9-6,  how do we find LL for a slender section?
As an external resource –A Beginner’s Guide to Structural Engineering