Last Updated on September 19, 2023 by Maged kamel

Product of inertia Ixy for the parallelogram.

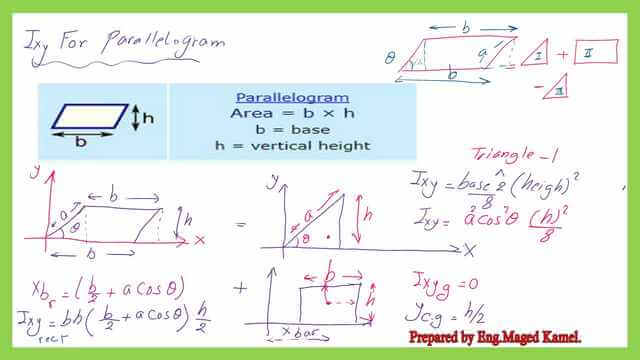
For the product of inertia Ixy for the parallelogram, we will consider that is composed of one triangle marked I and a rectangle marked II, but we need to subtract the area of one triangle marked III.

our x-axis is the horizontal axis passing by the lower base of the parallelogram, while the Y-axis is the vertical axis passing by the left corner.

Product of inertia Ixy for triangle and rectangular part.

We know already the product of inertia Ixy for the left triangle for which it is equal to the square of the base multiplied by the square of height divided by 8.

The base equals a*cos θ, where θ is the enclosed angle between the inclined length and the horizontal length of the parallelogram, please refer to the first slide image. the height of the first triangle equals h.

For the rectangle, the product of inertia about its Cg equals zero, because of symmetry.

To estimate the product of inertia for the rectangle about the X and Y axes, we need to find the horizontal distance x bar and the vertical distance y bar from the Cg to the left corner.

The x-bar is found to be equal to (b/2+a cos (θ), while the Y-bar distance equals (h/2). The product of inertia for the rectangle equals the product of area by x-bar by y- bar. The value is shown in the next slide image.

Product of inertia Ixy for a right triangle.

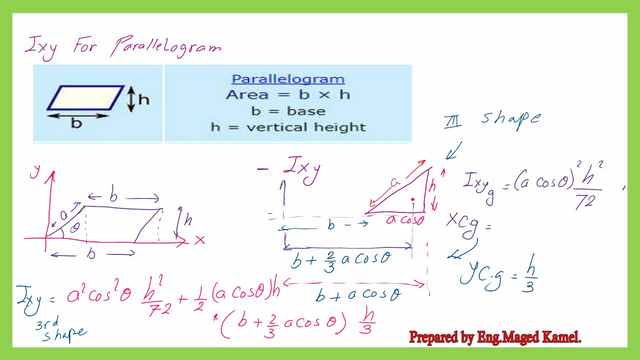
We will estimate the product of inertia Ixy for the third shape, the triangle, its product of inertia at its Cg is equal to the square of its base by the square of its height divided by 72.

The base is equal to (a cos(θ), and the height equals h.

The product of inertia Ixy at Cg=(a cos(θ))^2*h^2/72.

We need to add the product of area by x-bar by y-bar from the Cg to the left corner to the product of area by the area of the triangle equals (1/2)(a cos(θ))*h. X-bar and y- bar.

The final value for the product of inertia for the third triangle can be found in the next slide image.

In the next slide, all the products of inertia for the left triangle, rectangle, and the third shape, triangle are listed.

The product of the inertia of the Ixy-for the second triangle is to be subtracted from the sum of the product of the inertia of the triangle and the rectangle.

I have made a simplification for the common terms to reach a value for the product of inertia Ixy for the parallelogram.

The final value for the Product of inertia Ixy for the parallelogram.

The final expression for the product of inertia for the parallelogram can be found as equal to (h^2*b)*(3b+4*a*cos (θ)) divided by 12.

Since we can substitute for the height h as equals (a* cos (θ), then the final value for the Product of inertia Ixy for the parallelogram can be rewritten as equals (a^2*b*sin^2(θ)*(3b+4*a*cos (θ)) divided by 12.

For the square of the radius of gyration r^2xy, it can be obtained by diving Ixy /area, since the area of the parallelogram equals (b*a*sin(θ)).

The final r^xy equals (a*b*sin(θ)*(3*b+4*a*cos (θ)) divided by 12. the detailed estimation is shown in the next slide image.

Check the product of inertia for a rectangle as a special case of a parallelogram.

We can check the value of the product of inertia for a rectangle with base b and a height a since the rectangle is a special case of a parallelogram but setting the angle (θ) as equals 90 degrees. first the h=a *sin (90)=a.

The Ixy for the rectangle at the left corner can be found after substituting the equation of the product of inertia for the parallelogram and letting cos (θ)=0. the value will be equal (a^2)*b^2)/4, which we obtained earlier from post 5.

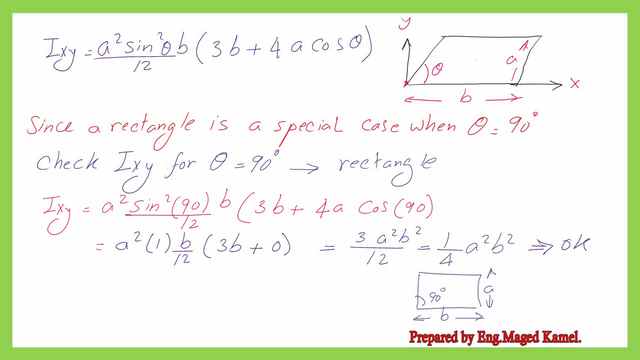
The final value for the Product of inertia Ixy for the parallelogram at the Cg.

The final value for the Product of inertia Ixy for the parallelogram at the Cg can be obtained by subtracting the product of the area of the parallelogram by (x-bar*y bar) from the final expression of the product of inertia at the y-axis.

We know that the x-bar value equals ( b+a*cos(θ)), while y bar=h/2=a*sin(θ)/2.

The final value for the Product of inertia Ixy for the parallelogram at the Cg can be found to be equal to (a^3*b*(sin^2(θ)*cos(θ)/12.

Check the product of inertia for a rectangle as a special case of a parallelogram at the CG.

We can check the value of the product of inertia, at the Cg, for a rectangle with base b and a height a since the rectangle is a special case of a parallelogram but setting the angle (θ) as equals 90 degrees.

Let h=a *sin (90)=a. the expression for the product of inertia as proved is equal to (a^3*b*(sin^2(θ)*cos(θ)/12. substitute for θ=90 degrees, we will find out the product of inertia for the rectangle equals zero, which matches the well-known fact that the product of inertia for the rectangle at the Cg equals zero.

For more information on the moment of inertia Ix for the parallelogram please refer to post 20.

For the moment of inertia for the parallelogram about the Y-axis, please refer to post 21.

For a useful external resource for the area, Cg, and inertia for the parallelogram, please refer to this link.