Last Updated on December 4, 2025 by Maged kamel
A solved problem 10-2 For Beam Adequacy For Shear.
This post has two parts. The first part discusses solved problem 10-2, while the second part discusses the nominal shear for steel beams based on CM#14 and specification 2010.
A solved problem 10-2, check shear adequacy.
This is solved problem 10-2 from Prof. McCormack’s book. There is a beam with a W section of W21x55 and Fy =50k. Check the adequacy of this beam to shear.
First, we will start with the LRFD design and estimate the ultimate load and the Ultimate shear. From the data in the next slide, the ultimate uniform load is 7 kips/Ft, and the ultimate shear value is 70 kips.

Table 1-1 shows all the relevant data for W21x55. A section of W21x55 is drawn, as shown in the small sketch on the left side. We can find the values of d, hw, and tw.
The enclosed web height h, or the distance between flanges less the fillets, equal to d-2*kdes hw equals 18.76” while the web thickness tw=0.375″.

The controlling factor for h/tw, as given by the AISC, is given by the equation h/tw=2.24*sqrt(E/Fy). Consider E=29000 ksi and Fy=50 ksi. The value equals 53.90.

The next slide shows the Nominal shear value for the steel beam. The coefficient of shear is termed Cv in the case of CM#14 and is termed Cv1 in the case of CM#15.

The ratio of h to tw equals 50.03 and hence less than 53.90.
The next step is to get the nominal shear for the section where Vn=Cv*0.60*Fy*(Aw*d), cv=1, Fy=50.0 ksi, A web=d*tw=20.80*0.375=7.80 inch2—the value of nominal shear Vn=0.60*50*7.80=234.0 kips.

For the LRFD calculations for section adequacy for shear stress, we have Cv =1, then φv *Vn=1*234.0 =234.0 kips, while Vul=88.0 kips, the section is safe.

The next slide includes estimates of the steel beam’s total uniform load and maximum shear value.

For the ASD calculations for section adequacy for shear stress, we have Ωv =1.5, then (1/Ω)Vn=(1/1.50)234.0 = 156.0kips, while Vt=(210+410)=60.00 kips, then the section is safe.

We will explain the AISC code provision for shear.
AISC specification provision for the design of Members for shear-CM#14.
Chapter G is the designated chapter for the design of members for shear.
Clause G-1 is for the general provisions. Item G2 deals with stiffened and unstiffened steel sections, including W, M, Hp, and S. The other sections not included in G2 are shown in G3, G4, G5, G6, G7, and G8. Please find the data in the next slide image.

There is a note for the steel shapes with h/tw that do not meet the specification requirement of h/tw<=2.24*sqrt(Fy), such as W44x230 and W40x149.

Cv value determination for shear of steel beams.

The factor kv is considered equal to 5 for webs without transverse stiffeners.

The value of Kc in the case of stiffened web.

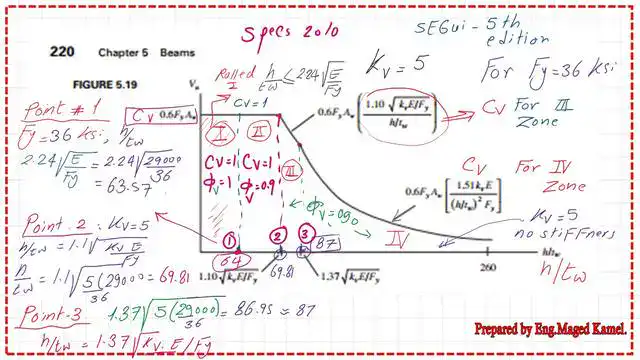
The relation between Vn and h/tw for Fy=36ksi.
The next slide shows the relation between h/tw and the Vn,the nominal shear value; there are four parts: part I is from h/tw value 0 to h/tw equal 2.24*sqrt(E/Fy), this zone has phi for shear phi value equal 1 and lambda-1.50.
Point 1 for the case of Fy=36 ksi is 63.57 and Cv=1, the Vn=1*(d*tw)*(0.60Fy).
The second part is between 2.24*sqrt(E/Fy) and 1.10*sqrt(k*E/Fy) Vn is constant. The third part is between 1.10*sqrt(k*E/Fy) and 1.37*sqrt(Kv/*E/Fy); the cv value is to be estimated, and there is a linear drop in the nominal shear value..
The last part is from 1.37*sqrt(Kv/*E/Fy) to h/tw=200; the CV value is to be estimated, and the nominal shear value has a curved drop.
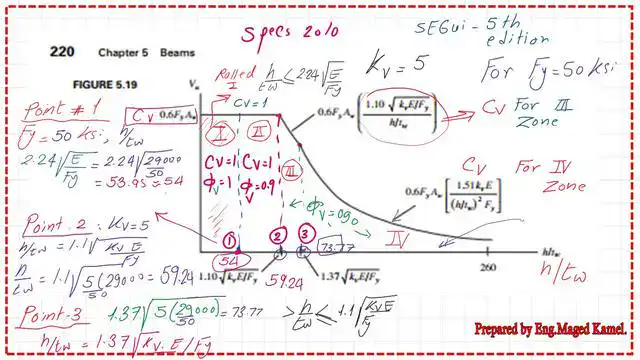
The relation between Vn and h/tw for Fy=50ksi.
Point 1 for the case of Fy=50 ksi is 53.95 and Cv=1, the Vn=1*(d*tw)*(0.60Fy). Point 2 value equals 59.24. Point 3 value equals 73.77.
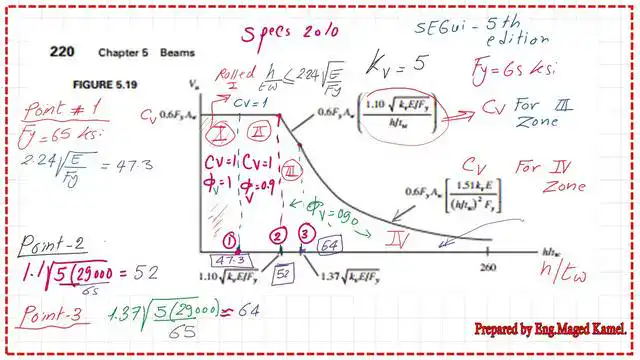
The relation between Vn and h/tw for Fy=65ksi.
Point 1 for the case of Fy=65 ksi is 47.30 and Cv=1, the Vn=1*(d*tw)*(0.60Fy). Point 2 value equals 52. Point 3 value equals 64.
This is a useful external resource for Shear Strength Limit State.
This is the next post, the solved problem-10-2, how to use table 3–2 for shear value?