Last Updated on June 7, 2024 by Maged kamel
A solved problem 2-22 for structural steel -shear stress estimation-part 2
For item b, the I section with a thickened flange will experience the maximum shear stress at the neutral axis.
The first moment of the area at point 1 equals zero since no area is enclosed, while the first moment at 2 equals area*cg distance=7*3*4.50=94.50 inch2. The easest way to calculate Ix is to consider the inertia of a bigger rectangle and deduct two inner rectangles. Please refer to the next slide image for more details.Ix value= 900 inch4.
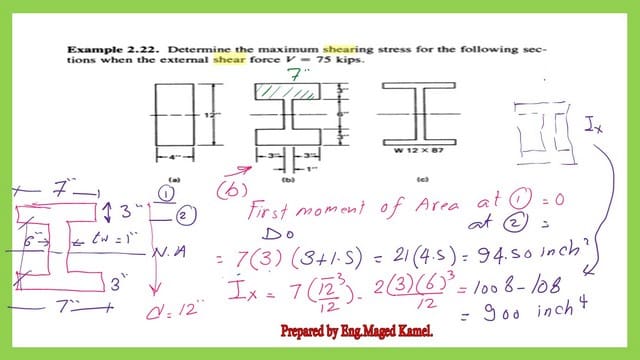
The first moment of the area at the N.A equals= 99.0 inch2. Ix=900 inch4,
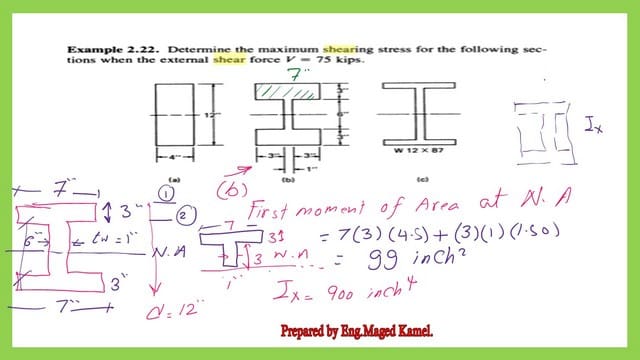
The next slide image shows a detailed estimation of the shear stress at point 2 and at the Neutral axis N.A. At point 2, there are two values for shear stress because we have two widths; the first width is 7 inches, and the second is 1″.
I
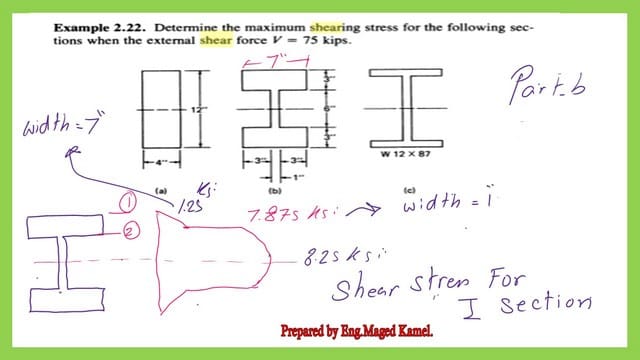
Immediately under the flange, the width decreases from 7″ to 1″, and the shear stress value jumps and is multiplied by 7; that is why the shear stress equals 7.825 ksi. The maximum value of shear stress equals 8.25 ksi.
Shear stress diagram for part c of the solved problem 2-22.
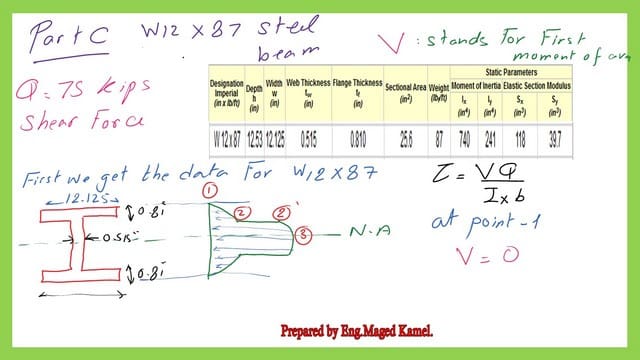
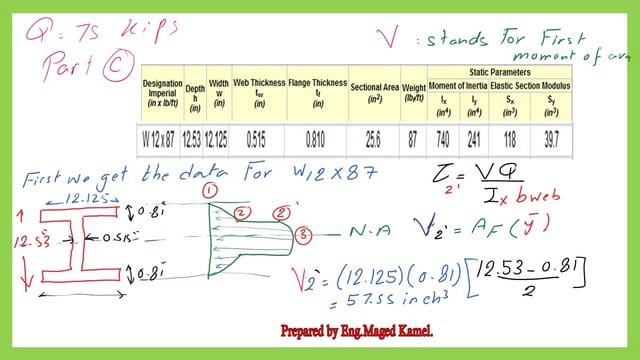
For item C, in the solved problem 2-22. For the I section W12x87, the relevant data was obtained from Table 1-1 for the depth of both flange and web thicknesses. the width of the flange=12.125″ and its width=0.81″.
While the web thickness =0.515″. The overall height of the W section =12.53″. Ix=740.0 inch4.
If we wish to draw the shear stress at points 1-2-2′ and 3, we will proceed as follows:
For point 1, the moment of area=0.
For point 2, the moment of area=Af*y CG to the N.A, the breadth=bf.
For point 2′, the moment of area=Af*y CG to the N.A, the breadth=bw.
For point 3′, the moment of area = Af*y CG +(A web)/2*ycg to the N.A, and the breadth = bw.
In the next slide, we can find the value of the first moment of the area at point 2.
The V value at point 2′, for the solved problem 2-22, equals 57.55 inch3.
The first moment of the area at N.A. equals 65.212 inch3.
The max shear stress value is 12.83 ksi at the N.A. If we evaluate as the web will carry the shear, then the average stress is 11.62 ksi.
AISC provision for shear.
The code specifies certain criteria for h/tw should not be <2.24*sqrt*(E/Fy); the Vn equation is shown. Aw=d*tW.
These are the relevant values for h/tw based on different steel grade values for zone 1. The list includes carbon steel Fy=36 Ksi ASTM A36 min Fy=36 ksi, and tensile=58-80 KSI.
In the next post, a solved problem 10-2 for beam adequacy for shear.
For a good reference-Shear Behavior. in Chapter 8 – Bending Members.A Beginner’s Guide to the Steel Construction Manual, 14th ed.