Last Updated on July 29, 2024 by Maged kamel
Cb the coefficient of bending part-3 for steel beams.
What are the cases where the old CB value equals 1?
Based on the old equation of CB, the value is given by the equation Cb=(1.75+1.05*(M1/M2)+0.30*(M1/M2)^2)<=2.30.
The CB old value must be equal to 1 in two cases. The first is a cantilever beam without a brace.
The second case for Cb equals 1 is a simply supported beam of length L acted upon by a uniform load w. It is braced at the two ends, but a moment value in the middle equals wl2/8, which is greater than M1 and M2.
Please refer to the image on the next slide for more information.

If we consider a simply supported beam with bracing placed at the midpoint to evaluate the value of Cb based on the old equation, for the part from left support to the brace at the middle, the CB value equals 1.75+1.05 (0/wl8)+0.30(0/wl2/8) 2=1.75.
The exact value of 1.75 will be given for the right part from the brace to the right support of the beam.
If we consider the case of a continuous beam of span L, where the braces are located at the supports, there are two equal and opposite moments. The two moments are opposite in direction, so the ratio of M1/M2 equals -1.
If we check the value of Cb, we find that it equals +1.

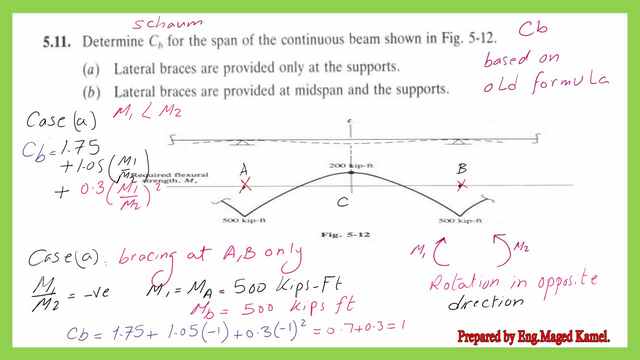
A solved problem for old Cb for a case of continuous beams.
I have included a solved problem from Schaum’s book. It requires determining Cb for the continuous beam shown in Figure 5-12.
The first case is where two braces are provided only at the supports.
There are three values of moments, the first-moment value is at the left support, point a which equals 500 ft. kips, the second-moment value is at the midpoint c and equals 200 ft. kips. The third-moment value equals 500 ft. kips at the right support point B.
For case a, we can find that the old CB value equals 1.
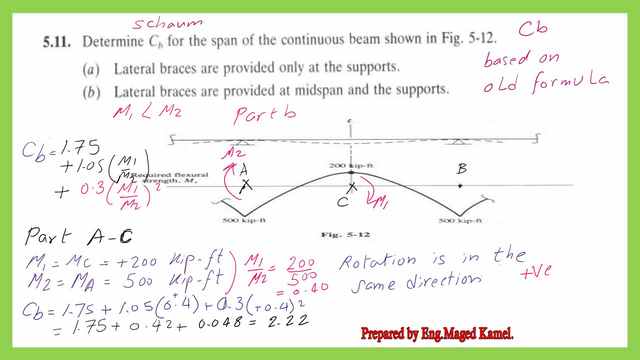
In the Cb The Coefficient Of Bending Part-3, for the second case, there are three braces, two at the supports and one brace at the midpoint of the span. Consider each part separately for part AC M2 equals 500 kips, which is more significant than M of 200 ft. kips; the ratio of M1/M2 equals +0.40.
We will apply the equation to get the old Cb value; we will find that the CB value will equal 2.22. the detailed solution is shown in the next slide image.
In the Cb The Coefficient Of Bending Part-3, we will check a summary of the part of the NCEES handbook reference 9.50 page 163; he started with LRFD and E=29000 ksi.
Beams for doubly symmetric compact I-shaped members, Φb=0.90, yielding Mn=Mp=Fy*Zx.
Where Zx is the plastic section modulus and explored the lateral-torsional buckling.
When Lb<=Lp, the Mn=Mp, the limit state of lateral-torsional buckling does not apply. When lb>Lp and less than Lr, then we will use the straight-line equation, Mn=cb(Mp-0.70FySx(lb-Lp)/(Lr-Lp)), where cb=12.50*Mmax/(2.5M-max+3*MA+4*Mb+3*Mc).
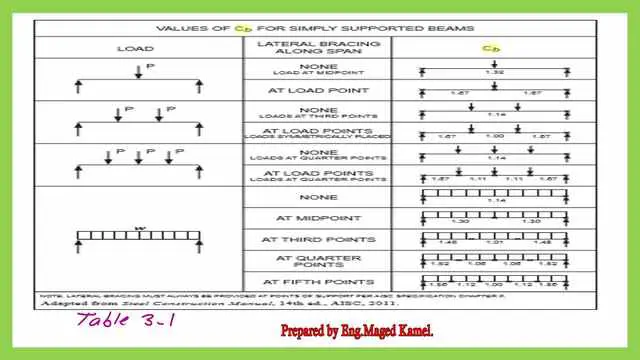
Table for the CB-coefficient of bending values for different loading conditions.
In the Cb The Coefficient Of Bending Part-3, we will check the different values of the bending coefficient based on the different loading conditions. This is part of the CB values, for which I have included a snapshot.

Next is a brief discussion of the nominal flexural strength, I quote, that the nominal flexural of the w shape is illustrated as a function of the unbraced length Lb.
The available strength is determined as Φb*Mn or Mn/Ωb.
The ultimate load is to be evaluated as 1.2 Wd+1.6 L, for the LRFD or the total load as estimated D+L in the case of ASD.
Then, the Φb*Mn >M-ult in the LRFD, or in the case of ASD, where Mn/Ωb> Mt.
Chapter F deals with flexural strength due to the moment in the AISC. The F1-1 section outlines the sections of chapter F and the corresponding limit states applicable to each member type.
Braced steel beam section.
For the braced and compact flexural Members, when flexural members are braced where Lb< Lp, where lb is the bracing distance, Lp is the plastic value for braces and the section is compact, λ<λp, whether in the case of flange or the case of the web.
Yielding must be considered in the member’s nominal moment strength, which is Fy*Zx.
Ubraced steel beam section.
In the case of the unbraced member Lb>Lp, have flange- width to thickness ratios such that λ>λp or have a web -to – width ratios such that λ>λp lateral-torsional and elastic buckling effects must be considered in the calculation of the nominal moment strength.
This intermediate zone or the straight-line relation starts from Mp.
It ends with 0.70*Fy*Sx, where λ>λp and lateral-torsional are to be considered after checking the Lb value, evaluating the lr, and then comparing. if lb>Lp Lb<Lr.
Noncompact or slender steel beam section.
If the section is non-compact or slender for width-to-thick members such that λ>λp, local buckling must be considered Available flexural strength for weak-axis bending.
A flexural member subject to weak axis bending is similar to that for strong axis bending, except that lateral-torsional buckling and web, local buckling do not apply. Bending about the y-axis will be dealt with with the same procedure as with the strong axis.

For more detailed illustrations in the CB, please follow this link. Flexural Limit State Behavior
This is the complete list of all posts related to Cb:
1-Introduction to Cb-Bending coefficient part-1 for the steel-post 17-previous post.
2- Cb-The coefficient of bending part 2 for steel beams-post 18-this post.
3-Cb-The coefficient of bending part-3 for steel beams-post 18a -next post.
4-Cb value-bracing at the midpoint of a beam-uniform load-Post 18b-Next post.
5-Cb value bracing at third points of a beam-U load-Post18C.
