Last Updated on September 6, 2026 by Maged kamel
- Approach to the compounding technique.
- A solved example is provided to illustrate the process.
- How to get the value of Fv1?
- How can the value of Fv2 be obtained for the compound interest of 6%?
- How can the value of Fv3 be calculated for the compound interest of 6%?
- Plotting the future values of the solved example.
- How can you get a future value of $1 after 1 year with interest at 100%?
Approach to the compounding technique.
Compounding technique: If interest is compounded, the interest earned at the end of the year is added to the principal and continues to compound until the end of the Time period. Future values are calculated using this compounding interest.
As interest rates increase, compounding interest also increases, which means if you want a large sum of Money, interest rates must be high. This is achieved by compounding in shorter periods.
We will start by discussing the compounding technique: converting simple interest to compound interest after one year, then changing the compounding period to less than one year. If we have a linear function represented by a line with equation y=mx+c, where m is the slope and c is the intersecting height with the Y-axis, the slope is constant.
The difference between ordinates is equal to (i*P0*n), where n=1.
Assume that the value of the function at Time t1=y1, at Time t2=y2, and at Time t3=y3.
The difference between these ordinates is constant, which means that y1-y0=y2-y1=y3-y2. To convert that linear function to an exponential function, we will set y1y0 = y22y1 = y33/y; our starting point for the exponential function will be at t = t1. From the linear function representing simple interest, we obtain the value of P0 at Time t0 and the value of FV1 at Time t1. The x-axis represents time in years for both graphs.
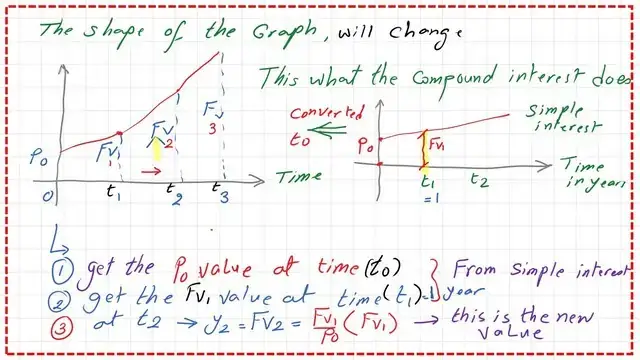
FV1 is the final value at Time t1, while P0 is the starting present value at Time t0. The left-side sketch represents the exponential form of compound interest, with the linear function holding Fv1/Fv0 = Fv2/Fv1 = Fv3/Fv2.
A solved example is provided to illustrate the process.
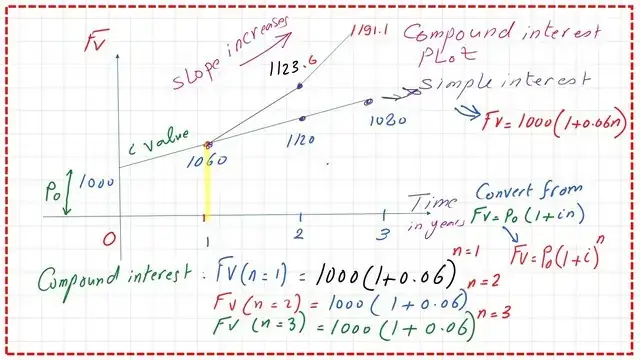
A solved example is given in which we have P0, and the present value of an investment deposited in a bank is $1000 at Time 0. The interest rate is 6%, a simple interest rate applied each year.
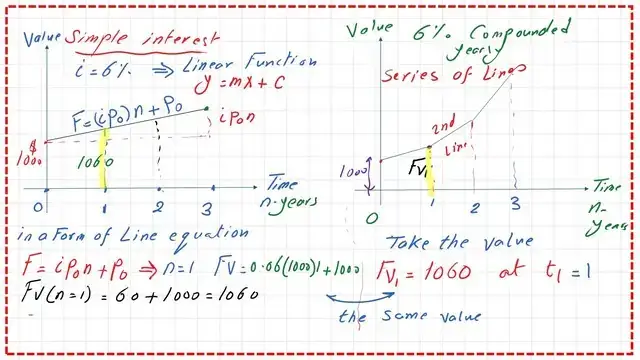
How to get the value of Fv1?
We are interested in the value of Fv1 at Time t1, where n represents the number of years. The future value FV1 at Time t1=P0+i *P0*i*(n)=1000+0.06*(1000*)*(1)=$1060. On the right side is the compounded graph of the same problem, too. P0 is still the present value at Time t0, and FV1 at Time t1 is the same, with the estimated value of $1060.
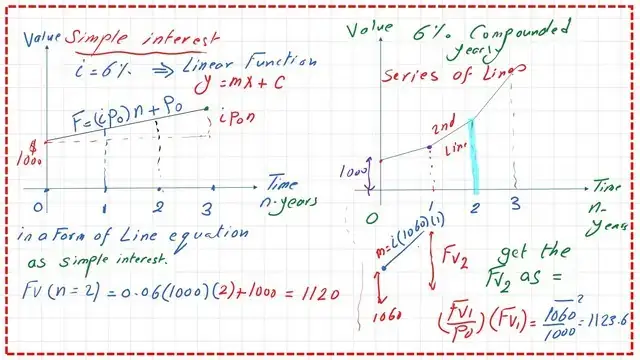
How can the value of Fv2 be obtained for the compound interest of 6%?
The future value of the Money at Time t2, which is FV2, will differ from the one estimated using the simple interest rate. FV2, due to compounding, can be estimated by multiplying (FV1/P0) by FV1. The Po value is $1000.
We have obtained the value of Fv1 as $1060. If we estimate the value of FV2, it will be = (1060/1000)*(1060)=$1123.60. Please refer to the next image for more details.
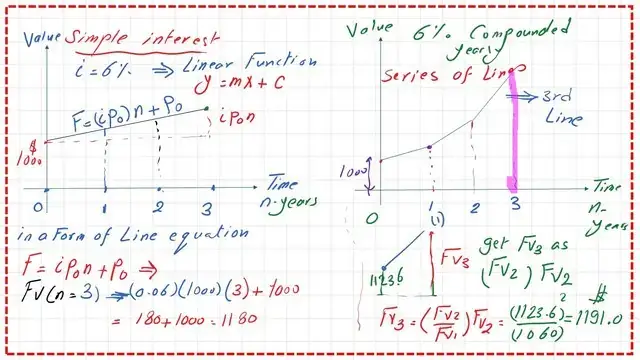
How can the value of Fv3 be calculated for the compound interest of 6%?
The future value of Money at Time t3, which is FV3, can be estimated by multiplying (FV2/P1*Fv2). If we estimate the value of Fv3, it will be (1123.6) 2/1060 = $1191.0.
Plotting the future values of the solved example.
The two graphs are drawn together for the invested Money at a simple interest of 6% for three years. The above graph shows the investment of $1000, but for compound interest of 6% compounded yearly.
The didifference ishat the slope isis greatern the case of compound interest.
How can you get a future value of $1 after 1 year with interest at 100%?
This is an application for converting from simple interest to compound interest. It is required to determine the future value of $1 after 1 year at 100% compounded yearly interest.
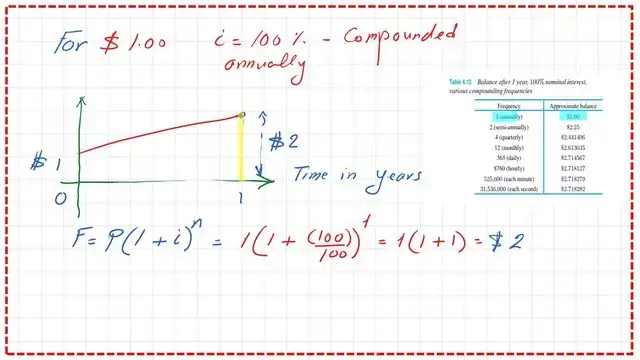
The future value of $1 after one year at 100% compounded yearly can be found to be $ 1 + (100/100)*(1)*(1) = $2.00. The value matches Table 4.13 for the compounded value of $1.
You can view or download the PDF of this post’s content by clicking the following button.
For a useful external resource, Engineering Economy is a good reference.
In the next post, we will derive the Expression for the different frequencies of compound interest—the following post 6a: Types of frequencies of compounding.