14a-Problem-6-8 for local buckling-CM#15 For HSS section

Last Updated on July 25, 2025 by Maged kamel

Solved Problem-6-8 for local buckling-CM#15 For HSS section.

Description of data.

The following slide image contains a brief description of the content of this post. I will resolve Example 6-8 from McCormac’s book for determining the available strength for a given HSS section, but this time the solution is based on CM#15, then we will confirm our answer by using Table 4-3 from Construction manual CM#15. The same problem 6-8 was solved in post 14, but using CM#14.

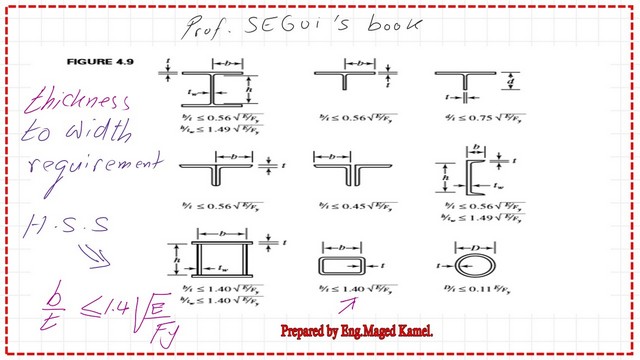
This is a brief description of sections that are not slender for compression members, from Prof Segui’s handbook, for which the slenderness ratios are included based on the shapes.

Detailed description for Solved problem 6-8 for local buckling.

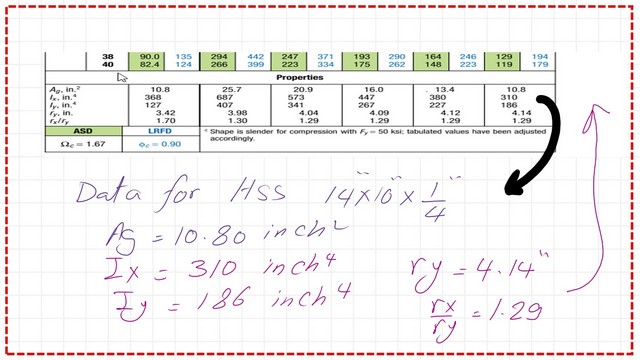
For the solved problem 6-8, determine the axial compressive design strength Φc Pn and the allowable design strength Pn/λc of a 24 ft HSS of 14x10x1/4 inch column section; the base of the column is considered to be fixed. From the first part of Table 1-11, we get the value of the area, which is equal to 10.80 inch2, h/t=57.10, Ix=310.0 inch4.

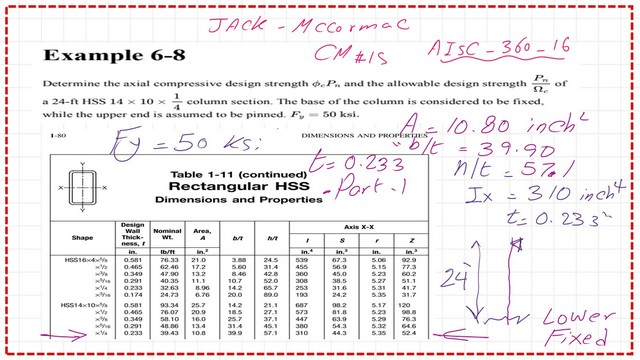
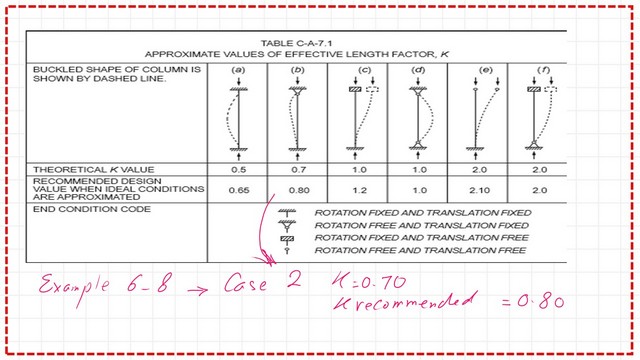
The upper end is assumed to be pinned—The yield stress fy=50 ksi instead of 46 ksi as in the same problem based on CM#14. The effective length factor k is 0.7 for the column, but the recommended value is 0.8. Refer to table C-A-7.1 of the specification. Please refer to the following slide image.

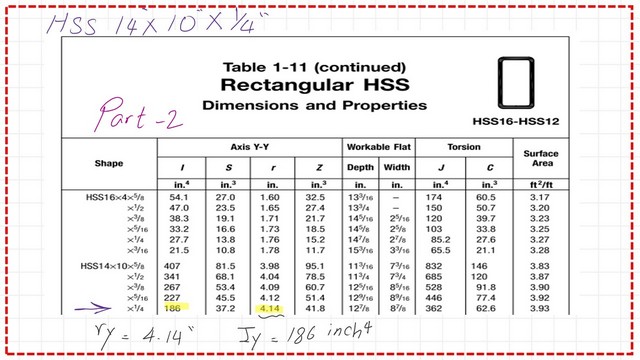
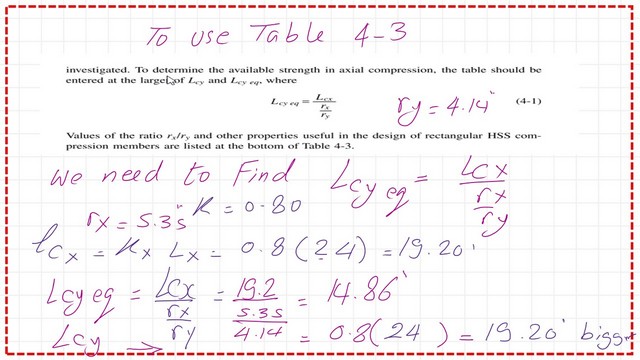
This is part 2 of Table 1-11 from which we get the values of ry and Iy, ry=4.14 inches, and Iy=186 inch4 for the HSS section 14x10x1/4 inches section.

Check which direction controls the design, whether X or Y.

The next step is to check which direction controls the design. For the x-direction, we estimate Lex/rx (0.8*24×12/5.35)=26.92.

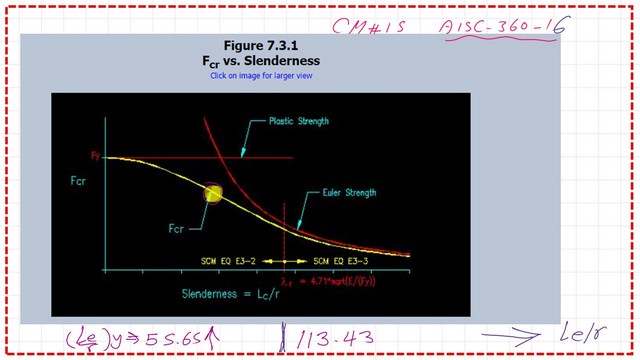
While in the y-direction, Ley/ry (0.8*24×12/4.14)=55.65. We select the bigger value; the design is governed by buckling in the Y-direction.

Find FE, check whether the HSS section is long or inelastic.

The next step is to check whether the column is inelastic or long; the limiting ratio is 4.71*sqrt(E/Fy )= 4.71*sqrt(29000/50)=113.43. Since ley/ry equals 55.65, which is less than 113.43, the column is inelastic. For the Euler stress, we have fe=Pi^2*E/(le/ry)^2; the Fe value equals 92.42 Ksi.

Check whether the HSS section is slender or not.

To determine whether the HSS section is slender, we check the b/t value against the limiting value for the slenderness ratio for a stiffened HSS section.

The limiting value equals (1.4* sqrt( E/Fy)=33.72. The b/t=39.90 from table 1-11, while h/t=57.10. The section is slender since b/t & h/t is bigger than 33.72. Please refer to the next slide image for more details.

The following slide image shows the relations between L/r and critical stress values and the curves used to estimate the critical stress.

The following slide image shows the hatched areas that represent the effective area for an HSS and W section that are slender; the modified b and h are to be estimated to get the value of that effective area.

How do we estimate the effective B and h?

Based on B4.1b for stiffened elements, it is recommended to calculate a modified b=b-3*td and modified h to be equal to h-3td where t design equals 0.233 inches, h=14 inches, and b=10 inches.

The value of b=10-3*(0.233) =9.301 inch, while h =14-3*(0.233)=13.301. Since the column is inelastic, we estimate fcr as equal to 0.658^ (50/92.42)*50=39.87 ksi.

Find the modified B value.

To determine whether we need to consider Be or the same b value, we need to check for λ value against λ, Fy, and fcr. based on the two equations E7.2 and E7.30.

Check for λr value, which is the ratio we get from Table B4.1, equals 33.72, against λ, which is equal to sqrt(Fy/Fcr)=33.76. Since b/t from table >37.76, then we need to adjust B and estimate be. Later, we will also check for h.

We need to estimate the elastic local buckling stress Fel, which is equal to (C2*λ/λ)^2*Fy. The value of Fel can be found to be equal to 68.01 ksi. We can proceed to estimate the value of Be using the E7.3 equation. The final value of be equals 8.974 inches.

Find the modified h value.

Check for λr value, which is the ratio we get from Table B4.1, equals 33.72, against λ, which is equal to sqrt(Fy/Fcr)=33.76. Since h/t from the table >37.76, then we need to adjust h and use equation E7-3.

We need to estimate the elastic local buckling stress Fel, which is equal to (C2*λ/λ)^2*Fy. The value of Fel can be found to be equal to 33.21 ksi, the value of Fel is different since the Lambda value is higher. We can proceed to see the value of He using the E7.3 equation. The final value of he equals 9.923 inches.

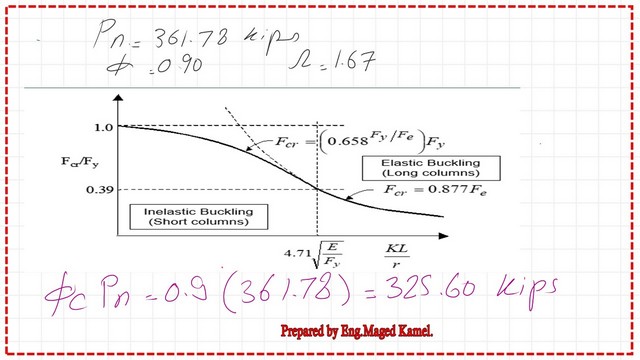
We can estimate the effective area of the HSS section, and it is found to be equal to 9.074 inch2. The nominal load Pn equals =Ae*Fcr=9.074*39.87=361.78 kips..

LRFD value for Nominal load.

For LRFD, Φc=0.90,Φc*Pn=0.9*361.78=217 kips.

ASD value for Nominal load.

For the ASD, Pn/Ωc=361.78/1.67=200.980 kips..

Use Table 3.1 to get the factored loads.

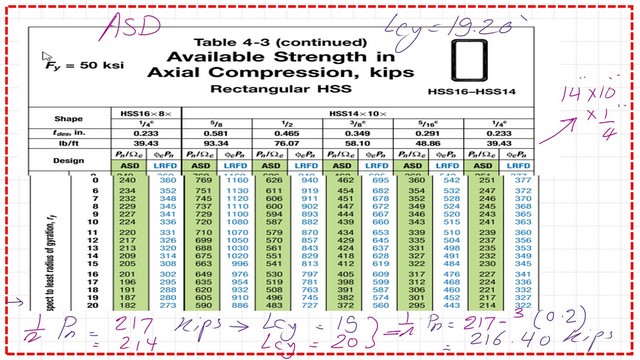
We will estimate the Ley for the lex, buckling length in x, we will divide by rx and multiply by rx, Lecy equivalent = 19.20 feet, while lcy=19.20 feet, which is bigger, and that is the length that will be used in Table 4-3.

The factored fcr based on the LRFD design is equal to 326 kips, after interpolation, very close to our estimate.

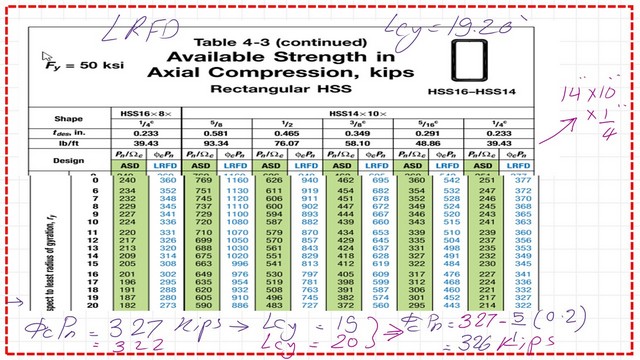
The factored fcr based on the ASDD design is equal to 216.4 kips, after interpolation, very close to our estimate.

In the footnote, you can check the gross area, Ix and Iy, and the ratio of rx/ry for the given section.

If you have the link, refer to the previous post: A Solved problem 5-3 for local buckling of columns.
The following post: A solved problem 6-19-4.

For a good external reference, find this link–Chapter 7 – Concentrically Loaded Compression Members.

 

 

 

 

.