Last Updated on March 13, 2024 by Maged kamel

Moment of inertia Iy-at Cg for a triangle.

Procedure to find the Moment of inertia Iy-at the Cg for a triangle.

1-To calculate the Iyg, we must first estimate the x-bar of the triangle, which is the distance from the triangle’s center of gravity to the Y-axis.

How do we get the X-bar distance for the triangle?

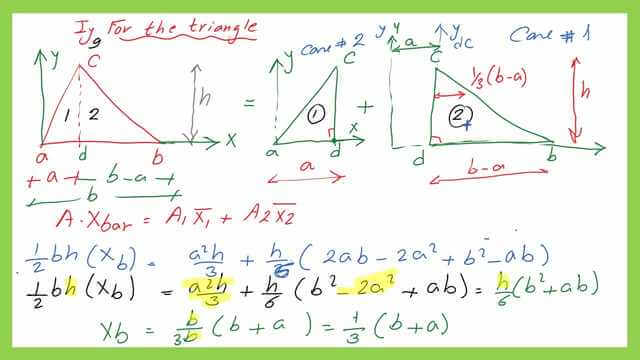
2-To get the x̅ distance for the triangles by using the first moment of area expression, estimate the A*x̅ which is the area of the triangle that will be equal to A1*x̅1 +A2*x̅2.

 The value of the first moment of area for the triangle can be estimated as 1/2(b*h) multiplied by x̅, which is the distance of Cgof the first triangle to the y-axis, the Y bar is passing by the external left edge. The first moment of the area can be expressed as an equal initial area multiplied by its CG.

From the y-axis, the Cg distance is equal to 2/3a. The first area is (1/2*a*h)*(2/3)*a) then we add the product of the second area, by the (2a+b/3). The first moment of area for the second triangle equals (1/2)(b-a)*(h)*(2a+b/3).

Add the sum of the first moments of areas of the right-angle triangles. To calculate the final value of the x bar, divide the estimated sum by the triangle’s area as follows: Please see the following slide images for further information.

The final x-bar distance for the triangle is calculated to be 1/3*(a+b). this distance is measured from the Y-axis passing by the left corner.

The calculations to get the moment of inertia Iy- at the Cg.

3-We can use the parallel axes theory to get the value of the moment of inertia Iy-at Cg-Iyg. We know that Iy=Iyg +(A*xbar^2).

4-To calculate the moment of inertia Iy-at Cg, deduct the product of (Axbar^2) from the value of Iy, which equals (bh/12)(b^2+a^2+ab).

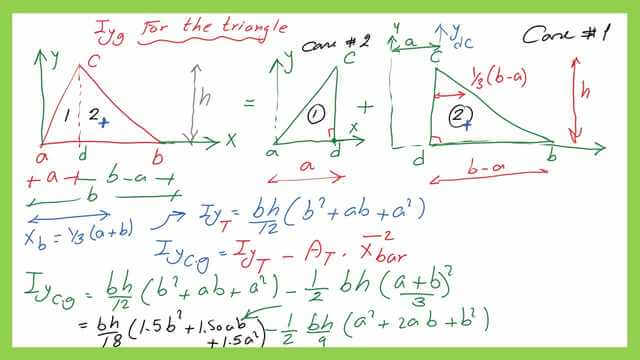
The moment of inertia Iy-at Cg is calculated as Iyg=1/18*(b^2-a^2-ab), where a represents the distance from edge point a to point d and b represents the distance between points a and b.

The square of the radius of gyration about the y-axis at the CG can be calculated by dividing the moment of inertia Iy-at Cg, Iyg by the area.

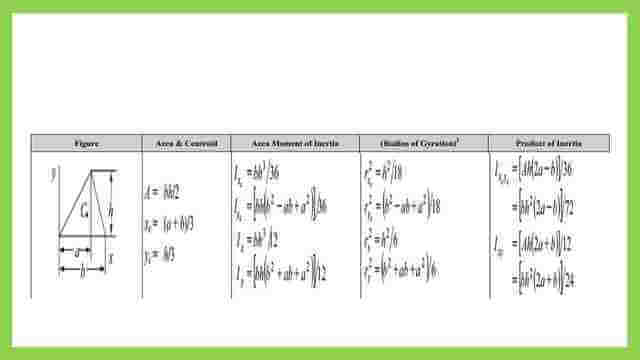
The square of the radius of gyration at the y direction for the triangle at the Cg is equal to 1/18*(b^2+a^2-ab). This is the list of inertia for triangular shapes quoted from the NCEES tables of inertia. from the table, we can find that the calculated moment of inertia Iy at the Cg matches with the given value at the table.

This is a link for the PDF file used in the illustration of this post.

For an external resource, the definition of the moment of inertia with solved problems, the 2nd moment of inertia.

This is a link for the next post, Product of inertia Ixy– for the triangle.