Last Updated on March 8, 2024 by Maged kamel

A solved problem-inertia value for a given direction.

In this post, we will introduce a solved problem-inertia value for a given direction. We will consider the same solved problem included in the previous post, to get the inertia value for a given direction. We are still in case 4, where the moment of inertia about X-axis Ix is lesser than the moment of inertia about Y-axis Iy and the product of inertia Ixy is negative.

The given solved problem includes an unequal angle of dimension 3 inches by 2 inches, and the thickness of the angle is (1/4) inch.

A solved problem-inertia value for a 30-degree clockwise direction.

In the solved problem, it is required to find the inertia values Ix’, Iy’, and Ix’y’ concerning new centroidal axes obtained by rotating the x and Y axes by 30 degrees clockwise.

From the previous post, we have a moment of inertia about the x-axis, That is Ix=0.39 inch4. The moment of inertia about the y-axis is 1.09 inch4. The product of inertia Ixy equals(-0.3798) inch4. The radius of Mohr’s circle equals 0.5166 inch4.

The angle φp1 value is 66.831 degrees, while the value of the angle φp2 equals to-23.169 degrees. The data of the solved problem is shown in the next slide image.

Using General equation-inertia value for 30 degrees clockwise direction.

We will use the general equation to get the moment of inertia Ix’ about the axis rotated 30 degrees clockwise direction. First, we will multiply the given angle 30 degrees by 2 to get the value of 2θ.

The two thetas will be equal to 2 alpha, and the 2α value will be taken as =-60 since the rotation is 30 degrees clockwise.

Ix’=(Ix+Iy)/2+(1/2)*(Ix-Iy)*cos( 2θ)-Ixy*sin( 2θ). We will plug in Ix=0.39 inch4. The moment of inertia about the y-axis =1.09 inch4. The product of inertia Ixy=-0.3798 inch4.

The next slide image shows the detailed estimation of Ix’s value. In the solved problem-inertia value Ix’ will be equal to 0.2361 inch4.

Iy’=(Ix+Iy)/2-(1/2)*(Ix-Iy)*cos( 2θ)+Ixy*sin( 2θ). We will plug in Ix=0.39 inch4. The moment of inertia about the y-axis =1.09 inch4. The product of inertia Ixy=-0.3798 inch4. The next slide image shows a detailed estimation of Iy’s value.

In the solved problem-inertia value Iy’ will equal 1.2439 inch4.

Ix’y’=(1/2)*(Ix-Iy)*sin( 2θ)+Ixy*cos( 2θ). We will plug in Ix=0.39 inch4. The moment of inertia about the y-axis =1.09 inch4. The product of inertia Ixy=-0.3798 inch4.

The detailed estimation of the product of inertia Ix’y’ value is shown in the next slide image. In the solved problem-product of inertia value Ix’y’ will equal 0.1132 inch4 as shown in the next slide image.

Mohr’s circle of inertia-inertia value-Ix’.

From the previous post, we have drawn Mohr’s circle of inertia, we have the radius of the circle R equal to 0.5165 inch4

The values of 2φp1 and 2φp2 are shown together with x-direction and y-direction. The relevant data of Mohr’s circle of inertia is shown in the next slide image.

We have given data on the direction of the oriented axes 30 degrees in the clockwise direction. to use Mohr’s circle we will consider twice the value of 30 degrees to be equal to 60 degrees, drawn in the clockwise direction from the x-axis which is represented by line OA in Mohr’s circle.

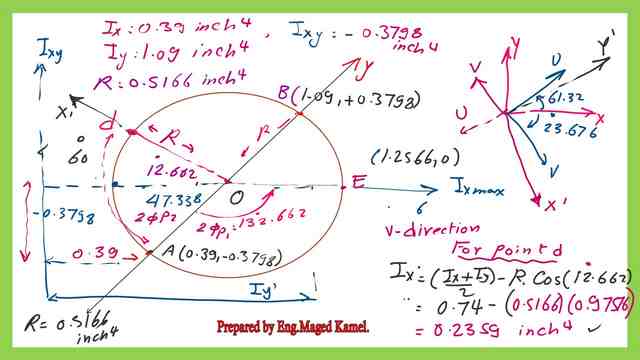
Moving 60 degrees in the clockwise direction will create point d.

The horizontal distance from point d to axis Ixy will give Ix’ value. Ix’ value will be equal to(Ix+Iy)/2-R*cos(60-2φp2).

The value of (60-2φp2) will be equal to =60-47.338=12.662 degrees. The inertia value Ix’ equals 0.2359 inch4 and is very close to the value of Ix’ estimated using the general expression.

Mohr’s circle of inertia-inertia value-Iy’.

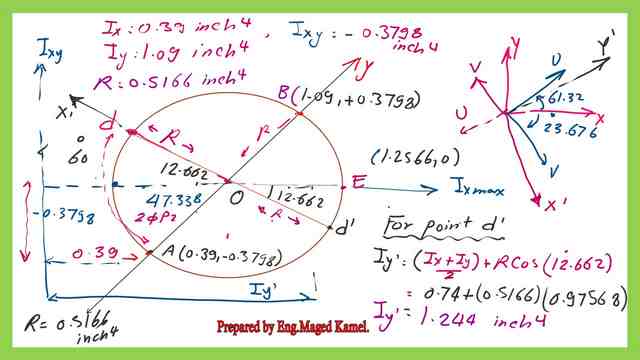
To estimate Iy’s value, we need to extend line DO to intersect with the circle at point d’. The horizontal distance from point d’ to the Ixy axis will be equal to the value of Iy’. The Iy’s value will be equal to(Ix+Iy)/2+R*cos((60-2φp2).

The inertia value Iy’ equals 1.244 inch4 and is very close to the value of Iy’ estimated using the general expression.

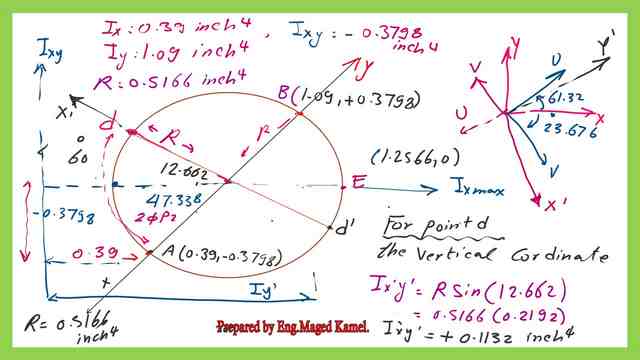
Mohr’s circle of inertia-inertia value-product of inertia Ix’y’.

To estimate the Ix’y’ value we need to estimate the vertical distance of point d to the horizontal axis Ix, Iy, Imax. Ix’y’=R*sin(60-2φp2). The product of inertia value Ix’y’ equals +0.1132 inch4 and matches the value of Iy’ estimated by using the general expression.

This is a link to a useful external resource. Calculator for Cross Section, Mass, Axial and Polar Area Moment of Inertia, and Section Modulus.

This is a link to the previous post-13-“A solved problem for Mohr’s circle of inertia case 4.