Last Updated on January 1, 2026 by Maged kamel
Moment of inertia Ix for a triangle.
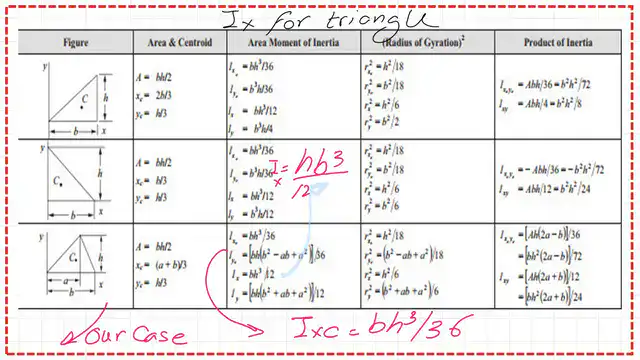
List of the area moment of inertia for a triangle.
The value of the area and Moment of inertia for the triangle is the third item in the shown table from the NCEES reference handbook-3.50. The shown table lists the values of Ix and Iy for the triangle.
Step-by-step guide for the calculation of Ix for a triangle.
1-For the moment of inertia Ix estimation for a triangle, we will consider that triangle, as composed of two right-angle triangles, for the first right-angle triangle, will be considered as case No.2. Please refer to the previous posts for the complete estimation for the values of inertias. For case number #2, the y-axis passes by the left corner Point a.
Case -2 right-angle triangle, which is the first right-angle triangle, has a base =a and a height equal to h, as shown in the next slide image.
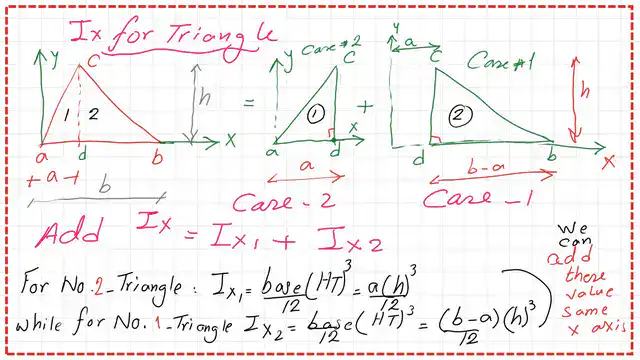
While another right-angle triangle will be considered as case no.1, it has a base equal to (b-a) and a height equal to h. We will list the inertia values as Ix1 and Ix2. Ix1 is the inertia at the x-axis for case No.2, while Ix2 is the value of the moment of inertia for case No.1 triangle.
2-For Ix estimation, adding the two values of inertia (a)*h^3/12+(b-a)*h^3/12 will give us
3-For the k^2x value, we will divide the Ix value /area of the triangle, so we get the y bar value for the triangle, which will be found as equal to h/3.
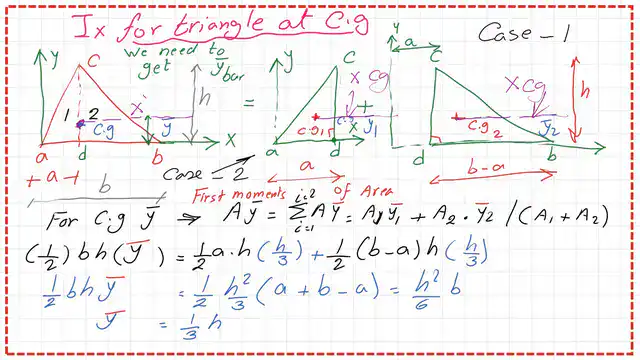
4- For the moment of inertia Ixg at the CG, we are going to estimate the y-bar for the triangles shown in the next slide from the first-moment area.
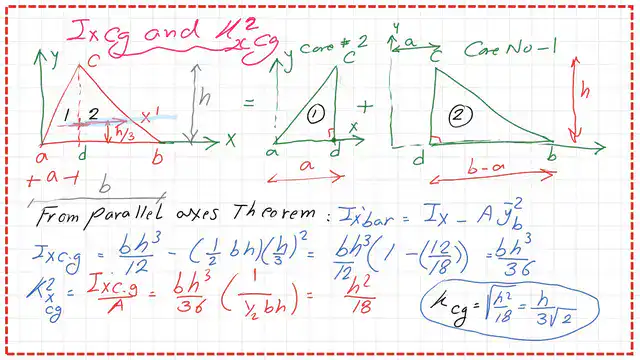
5- Ixg=Ix-A*y bar^2, after substitution, we will get the moment of inertia Ix for a triangle at the Cg as :
6-The radius of the gyration of the triangle can be estimated from the following relation. The square value of the radius of gyration for a triangle at the Cg can be found to be equal to h^2/18, where h is the height of the triangle.
You can download and review the content of this post through the following pdf file.
For an external resource, the definition of the moment of inertia with solved problems is the 2nd moment of inertia.
This is the next post, Moment of inertia Iy– for the triangle.