Last Updated on October 8, 2025 by Maged kamel
An Introduction to Solved problem 5-3 for local buckling of columns-CM#14.
A Solved problem 5-3 for local buckling of columns-CM#14 from Prof. Jack.C. Mccormac’s handbook Structural Steel Design -5th edition, the purpose of this solved problem is to show how we can find the value of the factored available strength by using both manual calculation and then verify by table 4-4 in the Aisc manual.

I have added Table 4-22 as an additional option.
Review of the equation used to differentiate between long and short columns.
As a review, first, we have to check whether the column is long or short by using equation 4.71sqrt(E/Qfy) in the case of KL/r >4.71sqrt(E/Qfy).

The column is long. if kl/r> 4.71*sqrt(E/Q*Fy), else the column is short if the K*l/r<=4.71*sqrt(E/Q*fy).
If the column is short, proceed to check the local buckling. In our case, the hollow steel section is a stiffened element for the flange and web; only one equation will be used.
Refer to item d. See B-3, which includes how to measure the b length of HSS and the definition of both b and h.

A Solved problem 5-3 for local buckling.
For the solved problem 5-3, An HSS section 16x16x1/2 inch, with Fy =46 ksi, is used for an 18-foot column with simple end supports. Determine Φc*Pn and Pn/Ωc, with the appropriate AISC equations, repeat part a) Using 4-4 in the AISC Manual.
We refer to Table 1-12 for the properties of the Hollow sections. Select HSS16x16x ½. The area is 28.3 inches 2. fy=46 ksi. The design thickness of the square HSS=0.465 inches and the radii of gyration about both axes x and y equals 6.31 inches.

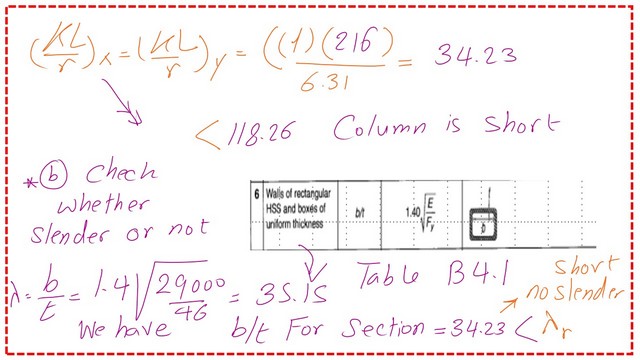
The next step is to check whether the column is short or long by finding the limiting KL/r value.

While Kl/r/rx=Kl/ry=34.23 is less than 118.26, the column is short, KL=1*18 *12. For the slenderness ratio, according to item 6 for HSS, λr=1.4*sqrt(E/fy)=1.4*sqrt(29000/46)=35.15, which is bigger than Kl/r, so the section is nonslender.
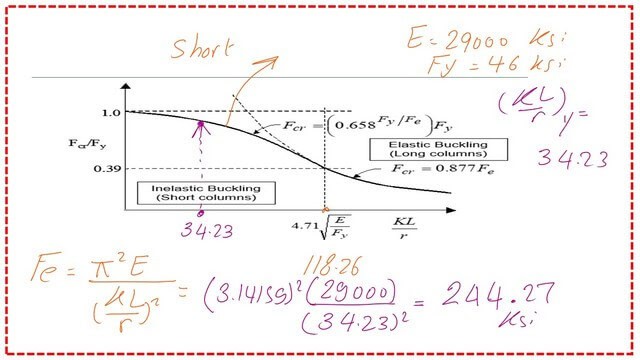
What is the value of The Euler stress?
Since the column is a short one, the Euler stress equals Pi^2*E/(KL/r)^2, which equals 244.27 ksi, please refer to the next slide image for more information.
Determine the factored available strength.
We will estimate Fcr =0.658^(46/Fe)*fy, with no Q in the equation since Q=1. We need to estimate Fe, Fe=Pi^2E/(KL/r)^2, Fe= (22/7)^2(29000)/(34.23)^2 =244.4744 ksi, back to fcr=0.658^(46/244.4744)(46)=42.516 ksi.
Then, for LRFD, ΦFcr for ASD, use Fcr/Ωc. For the nominal load Pn=Fcr*A=42.51*28.3=1203 kips, for LRFD, our Φc=0.9.
Then Φ*Pn=0.9*1200=1083 kips. for the ASD, since Ωc=1.67,Pn/Ωc=1200/1.67=720 kips.

Using Table 4-22 as an additional option for solving problems 5-3.
For Table 4-22 for available critical stress for compression members, page 4-322 Aisc 14 edition manual, we have kl/r=34.23, from Fy=46 ksi.
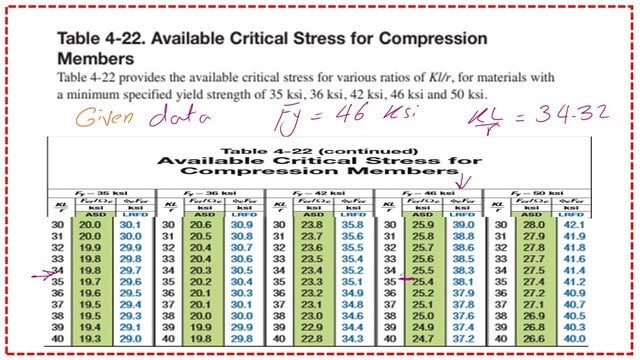
From the left side of the table, log in with 34.24. In between 34 and 35, for kl/r=35, we have 38.3 ksi, while for kl/r=34, we have 38.1. By interpolation, our final value ΦFcr=38.254 ksi, which is the stress value. Converting it as a load multiplied by the area, which is 28.3 inch 2, or Φ*Pn=1082.59 kips.

From Table 4-22, The stress, Fcr/Ω is between 25.5 and 25.4, by interpolation= 25.477 ksi, then multiply * area which is 28.3 inch2, Pn/Ω=721 kips, same as the estimate earlier. The values were driven first by using equations and then by using Table 4-22.

Use Table 4-4 as part b for the solved problem 5-3.
Table 4-4 is close to Table 4-3; it is used to determine the factor available strength, but is assigned to square HSS sections. It uses the effective length value Kl in the Y-direction and needs to be converted from Kl at x to Kl at Y.

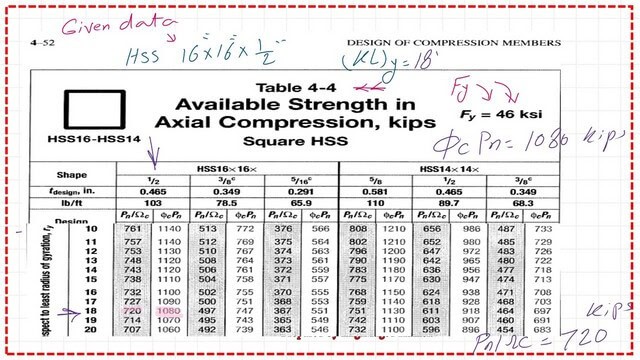
For part b, where Table 4-4 is required, it is for the square HSS. We have Fy=46 ksi, HSS is 16x16x1/2 inch, and K*l in the y direction =18′.
We can log in to Table 4-4 and select The KL at y=18′. Then, from the column 16x16x1/2″, we get the LRFD and ASD values for the column. Please refer to the following slide.
The calculation for the load is based on both the LRFD and ASD design.
This is the PDF file for this post.
If you wish, refer to the previous post: A Solved problem 5-2 for local buckling of columns.
For a good external reference, find this link–Chapter 7 – Concentrically Loaded Compression Members.
This is a link for the next post, solved problem 6-8