Last Updated on April 28, 2024 by Maged kamel

Solved problem 4-6-block shear for a C-Channel-1/2.

Topics included in our discussion are shown in the next slides.

The solved problem 4-6 is the same as the solved problem 4-4, which we considered in the previous post, but it is required to include the block shear.
The solved problem 4-6 are from Prof. Abi O. Aghayere’s handbook-3rd edition..

We need to determine whether the channel and gusset plate are adequate for the applied tension ultimate Load, but we also have to consider the block shear.

Consider block shear demands that the plate’s breadth is such that block shear, combined with the failure plane depicted in Figure 4-12, governs the plate’s design.

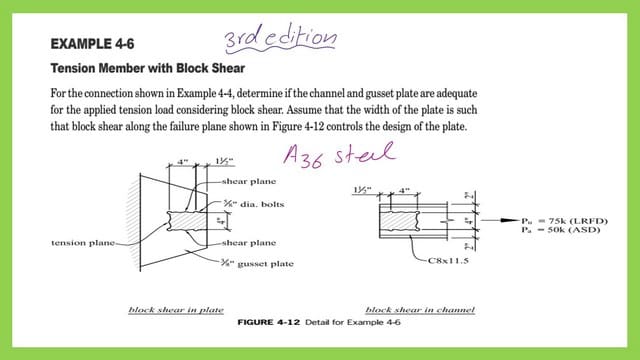
If we look closely at the C channel after it has been split, we can see that the hatched shape is torn from the original shape, there are four bolts, and a route has been created for the separated component. The hatched area length is 5.50″ by 4″ in height.

The calculation for Agv, Anv, and Ant is for the channel.

 We will perform the necessary calculations for the C channel to check the Block shear strength.
 1- We have one plane acted upon by tension force for which Agt is the gross area for tension, and the area Ant is the net area for tension. The section is perpendicular to the direction of the applied force. the height of this section=4″ and the web thickness =0.22″.

The channel’s gross area is 3.37 inches2. The gross area under tension estimation is written as Agt=4*0.22=0.88 inches2.
For Ant, which is the net area under tension, deduct two halves, which is one diameter of (5/8″+1/8″)=6/8″, and then multiply by the web thickness. The net area for C channel Agt- the sum of holes *t-web=0.88-((0.22*1)*(6/8))=0.715 inch2.   

Please refer to the next two slide images for the details of these calculations; they show the number of hole diameters for both tension and shear. 

2—The shear force component acts upon two planes, for which Agv is the gross area for shear, and Anv is the net area for shear. For the estimation of  Agv=(2*5.50*0.22)=2.42 inch2, for the net area in tension, Ant deducts 3 diameters area of 3*(6/8)*(0.22)=2.42-(54/64)=1.925 inch2.    
    

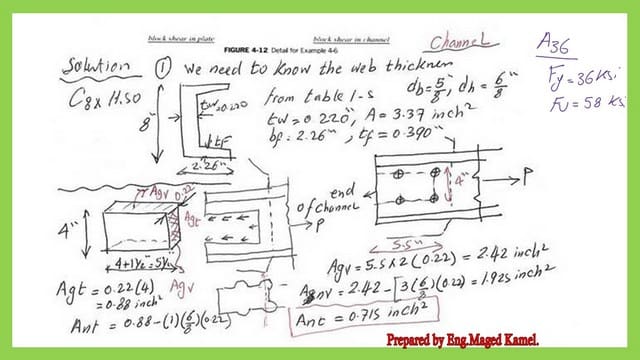
The calculation for block shear for the channel.

We will list all the values of Agv, Anv, and Ant that we estimated earlier. The steel is A36, with Fy=36 ksi and ultimate stress Fu=58 ksi.

Based on the LRFD design, φ equals 0.75 for shear yielding and tension rupture. Multiply Phi by (0.60*Fuy*Agv)+UBS*Ant*Ful).

Based on the LRFD design, we have φ equals 0.75 for the case of shear yielding and tension rupture. Multiply φ by (0.60*Fy*Agv)+UBS*Ant*Ful). We will substitute in the equation that the design nominal block shear value will equal 70.31 kips, as shown in the next slide image.

Based on the LRFD design, we have φ equals 0.75 for the case of shear and tension rupture. Multiply φ by (0.60*Fu*Anv)+UBS*Ant*Ful). We will substitute in the equation that the design nominal block shear value will equal 81.35 kips.

Select the min value of 70.31 kips and check against the value of P ult.We will find that the design strength in block shear is less than the Ultimate load, so the C channel is inadequate to carry the ultimate load.

In the next post, we will continue to solve problems 4-6.

The post will include all the necessary data for estimating the block shear for the Gusset plate and checking its adequacy in both LRFd and ASD. We will also continue to check the adequacy of the C channel for the total load.

There is a very useful external link-Block Shear Rupture.
The next post is a Solved problem 4-6-block shear for a C-Channel-2/2.