5A-Practice problems with linear approximation

Last Updated on January 19, 2026 by Maged kamel

Practice problems with linear approximation.

This is practice problem #3; it requires finding the approximate value of the third root of 8.

In Practice problem #3, it is required to obtain the approximate value of the third root of 8, the third root of 8.20, and the third root of 25.00. Here are the steps:

Part 1 of Practice problem #3-Practice problems with linear approximation.

1-Our starting point is chosen to be a₀=8.00, in the first case let b₀= 8.00.
2- The function value at x=8 will f(x)=2.00.
3-The differentiation of f(x)will be=1/3*(x^(1/3)-1)=1/3*x^(-2/3), the slope value at x=8, will be=(1/3)*(8)^(-2/3)=1/12.

4-Use the linear approximation expression and get L(x=8) =f(8)+(y’*(x_b-x_a), a is the starting point where x=8.00 and ending point=8.00, the term relates to the slope will be=0.
5- the linear approximation L(x=8)=2.00+(1/12)*(8.00-8.0))=2.00. 6-The exact value is the approximated value + error, the exact value is equal to 2.00, and the approximated value=2.00.

7- The error value=2-2=0.00. Refer to the previous slide image for more details.

Part 2 of Practice problem #3, the first problem of the Practice problems with linear approximation.

Solved example #3: It is required to get the approximate value of the third root of 8.20.
1-Our starting point is chosen to be a₀=8.00, in the first case b₀= 8.20.
2- The function value at x=8=2.00, this f(x=a).
3-The differentiation of f(x)will be=1/3*(x^(1/3)-1)=1/3*x^(-2/3), the slope value at x=8, will be=(1/3)*(8)^(-2/3)=(1/12).

4-Use the linear approximation expression and get L(x=8) =f(8)+(y’*(x_b-x_a), a is the starting point where x=8.00 and ending point=8.20.

5-L(x=8.20)=2.00+(1/12)*(8.20-8.0))=2.0166. ated value=2.00.
6-The exact value equal to the approximated value + error, the exact value is 2.01652, the approximated value=2.0166.

Part 3 of Practice Problem #3: Practice problems with linear approximation.

In Part 3 of Practice Problem #3, the approximate value of the third root of 25.0 is required.
1-Our starting point is chosen to be a₀=8, in this third case the value of b₀= 25.
2- The function value at x=8=2.00, this f(x=a).
3-The differentiation of f(x)will be=1/3*(x^(1/3)-1)=1/3*x^(-2/3), the slope value at x=8, will be=(1/3)*(8)^(-2/3)=(1/12).

4-Use the linear approximation expression and get L(x=25.0) =f(8)+(y’*(x_b-x_a), a is the starting point where x=8.00 and ending point=25.

5- The linear approximated value at 8.2 will be written as L(x=8.20)=2.00+(1/12)*(25.0-8.0)=3.4166.
6-The exact value is the approximated value + error; the exact value is 2.92424, and the approximated value is 3.41666.
7- The error value=(2.92424-3.4166)=-0.49266.

The detailed estimate for L(25) is shown in the following slide, along with the error value.

Practice problem #4– the second problem of the Practice problems with linear approximation.

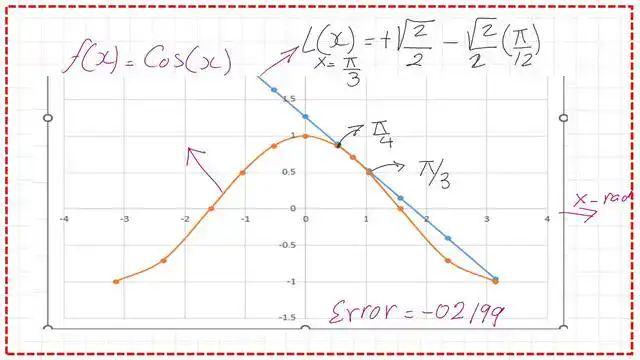
Practice problem #4: for the linear approximation of f(x) = cos(x) at the initial point PI/4, estimate the linear approximation at x = PI/3. The solution can be done through the following steps:
1- We need to estimate the function value at the starting point a, which is cos(PI/4)=0.707.
2- Get the slope at x=PI/4 of the function, f'(cos(x))=-sin(x), when x=Pi/4.

3- Get the value of y’ at x=PI/4, which is the starting point, it will be f'(x= PI/4)=-sin(PI/4)=-0.707.
4-Use the linear approximation expression and get L(x=Pi/3) =f(PI/4)+(y’*(x_b-x_a), a is the starting point where x=(Pi/4), while x_b is the point for which we want to estimate the Y value, which is =Pi/3.

5-L(x=Pi/3)=0.707+((-0.707)*(PI/3-PI/4))=0.52199.
6-The exact value= the approximated value + error, the exact value is cos(Pi/3)=0.50, the approximated value=0.52199.

7- The error value=0.50-0.52199=-0.02199
8- For the absolute value of the error %, divide by 100, then error%=4.40%.

The following graph shows the f(x), which is cos(x), and the line of L(x) that passes through the x0=Pi/4 point.

The PDF data for the previous post and this post can be viewed or downloaded through the following document.

The next post is about the Newton-Raphson method. The method is another root-finding method.

Here is a useful link to the Linear approximation calculator-e math help.