12-Solved problem: Future value for uniform series deposits.

Last Updated on September 7, 2026 by Maged kamel

Solved problem: How do we find the future value for uniform series deposits?

Future value for uniform series deposits with given n, I, A.

The solved problem is quoted from William G. Sullivan’s book Engineering Economy, 16th edition, Chapter 4. It can be written in Engineering Economy in two ways. The first way deals with the lending-and-borrowing point of view. A is drawn downward as a deposit with a negative sign (-A). The second way is to describe the matter regarding the Equivalence principle.

Suppose eight annual deposits of $187.45 each are placed in an account. How much Money has accumulated immediately after the last deposit?

The Money the man will receive will be denoted by F as a future value and drawn upward. This future value is an inflow. The interest is 10% annually. The same problem can be asked regarding the Equivalence: What amount at the end of the eight years is Equivalent to end-of-year payments of $187.45 each?

The Timeline is drawn in years, with eight downward payments represented by symbol A At the end of the eight years, there is an upward arrow for the future value F is unknown F is the amount to be received due to the investment of 8 annual deposits The interest rate is 10%.

We will use the known formula to get F for a given A; the equation will be written as F = A*(F/A, i,n). A will go with A, as both sides are identical.

F=A*(F/A,10%,8). First, we will substitute A’s value, $187.45, into the equation.

Use the Cash Flow Moments method to find the future value of a uniform series of deposits.

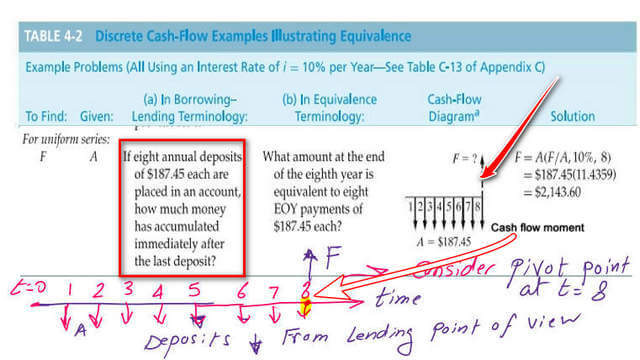
If we use the concept of Cash Flow Moments, we start by writing the given data as AAA = $187.45, I = 100%, n = ?, with F unknown.

Take a Moment about a pivot point at n=8 and write that the sum of all moments equals zero F*(1+i)^0-A*(1+i)^7, the Moment of first A is considered about a right point with time=8-1=7, A is minus, and the distance raised to the power with a positive sign, the second Moment due to the second A will be -A*(1+i)^6.

The third moment due to the third  A will be-A*(1+i)^5-A*(1+i)^4-A*(1+i)^3-A*(1+i)^2-A*(1+i)^1-A*(1+i)^0=0.

We simplify the sum of the elements by setting (1+i) = 1.10, and A is a common factor across all terms. I consider the corresponding exponent value.

The first exponent is 7, the second exponent is 6, the third exponent is 5, and so on, with a decrease of 1 for the next term.

we can get F=A*((1.1)^7+(1.1)^6+(1.1)^5+(1.1)^5+(1.1)^4+(1.1)^3+(1.1)^2+(1.1)^1+(1.1)^0. The value of (1.1)^7 is 1.9487, while (1.10) ^6 = 1.7715 and (1.1) ^5 = .6105. We will check the number of exponents as 8 values.

Finally, we get (1.9487+1.7715+1.6105+1.4641+1.331+1.21.1+1). The mean of these values is 11.4358.

We will multiply the previous value by A’s value, which is 82.45. Finally, we get F=$2143.60.

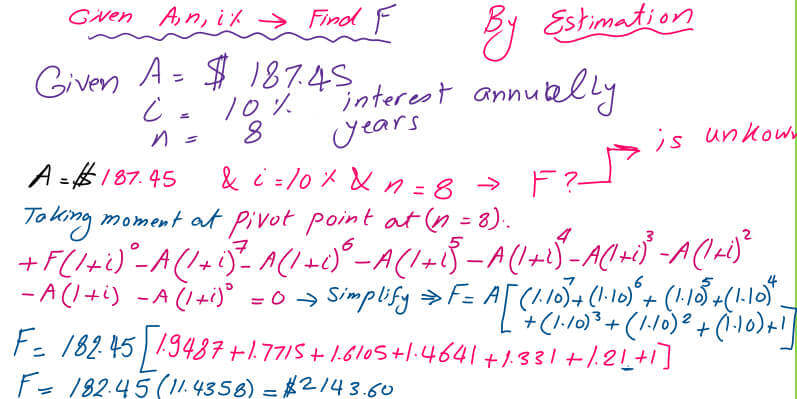
For future values for uniform series deposits, use the Expression for F/A.

The Expression of F/A  is used for a given A, and it is required to estimate the present value.F/A is equal to ((1+i)^n-1/(I).

The reciprocal of F/A will be A/F, and the A value for a given F value or future value can be obtained A/F=(I)/((1+i)^n-1)).

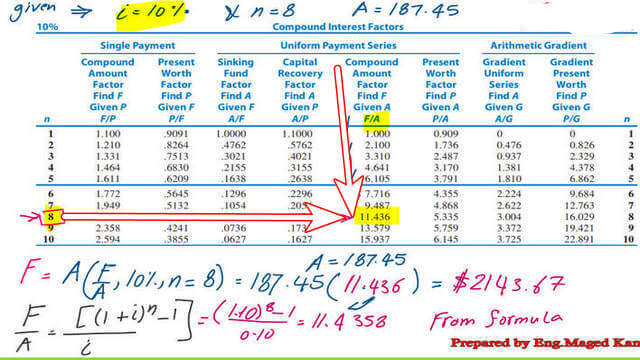
The future value F of a uniform series of deposits at an interest rate of 10% is determined using the interest table.

We need to estimate the value of F/A using a table with an interest rate of 10% for n = 8 years Before starting to use the table, first, we will use the Expression for F/A, which is equal to ((1+i)^n-1)/i We have i=10% and n=8  The value of F/A=((1.10)^8-1/(0.10)=11.4358 and can be approximated to 11.436.

If we wish to use the table, we select the 10% interest rate and use the title ‘uniform payment series’. The compound amount factor is F/A. We g down until the horizontal line intersects at n=8.. The intersection will give a value of 11.436.

This is the formula F=A(F/A,i=10%,n=8)=$187.45*11.436=$2143.67.

This is the formula F=A(F/A,i=10%,n=8)=$187.45*11.436=$2143.67.

For future values F in a uniform series of deposits, use the Excel function FV.

I can use an Excel sheet to list the necessary elements, arranged according to the generic formula for the FV function, which calculates the future value.

The Excel function is FV(I, A). The F/A name is a uniform series compound amount. The ter A/F is the name of a sinking fund; find A with a given F. This is the equation used to determine the A/ value. This is the standard notation: A = F(A/F, i, n).

We write Fv, then open parentheses (rate, periods, payment). For example, we can write Fv(10%, 8, -2.45). The payments are outflows, which is why they are negative. The result is a positive F value as inflows.

This serves as an alarm that you have deposited; use a negative sign to make the output positive, and you will get an inflow. Use an EExcel heet. The first cell is the rate = 10%, for example, C19. Then we write n in years in the next cell (C20), with n=8.

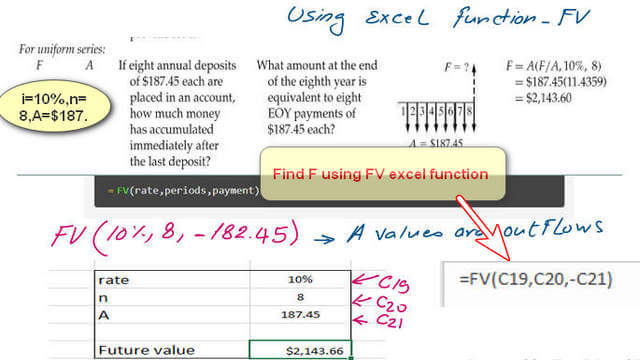
The A value is (+187.45) in cell C21.In the next cell, C22, we will enter the future value using the built-in function =FV(C19, C20 -C21). The result is $2143.66.

The PDF file for this post can be viewed or downloaded from the following link.

This is a good link – Engineering Economy: A good reference

The following post, Post 13, will discuss solved problems and deposit values for uniform series.