13-Solved problems, Deposit value for uniform series.

Last Updated on August 28, 2024 by Maged kamel

Table Of Contents

How do you find the deposit value, A, for uniform series?

How do you find the deposit value, A, for uniform series?

The first solved problem is to find the deposit value A for uniform series in terms of n, I, and F.

The title is College Savings Plan: Find A, given F, N, and I. F is the future value, N is the number of years, deposits, and time periods, and I is the interest.

You want to set up a college savings plan for your daughter, who is currently 10 and will attend college at age 18.

She needs at least $100,000 in the bank, which she must deposit.

The bank gives a rate of interest equal to 7%. Deposits are made in equal amounts at the end of each year. This is the case for the uniform series or A. The factor used (A/F) is called the sinking fund factor.

You need $100,000. This sum is the future value, A is unknown, given n and interest rate i%. The N value is eight deposits in eight years and i=7%.

The first solved problem, find the deposit value for uniform series -using cash flow moment.

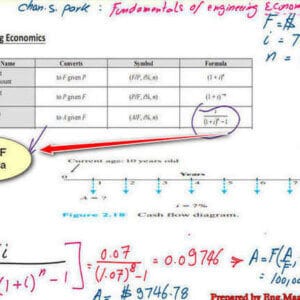
Suppose we use the cash flow moment method at a pivot point, t=0. The moment caused by the future value F will be equivalent to that caused by the uniform series of deposits at the same point.

To get the moment due to the future value, it is equal to F as positive, and the point is at the left side of F; the moment arm to pivot point t=0 will be(1+i)^-8. The moment value is $100,000*(1.07)^-8.

For the moment, this is caused by the uniform series of deposits. It will be as -A*(1+i)- 8+ (-A)*(1+i) -7 and so on until we complete the deposit expression. The sum of moments is zero. After adjustments, the result can be found as A multiplied by 5.97129.

The product of A*5.97129 will equal $100,000/(1.07) 8=$100,000/1.7181. We simplify the result as 100,000/10.2598=$974.78. The final value of A is $974.78, to be paid at the end of each year for 8 years to get the future value of $100,000.

Use cash Flow moment at pivot point t=0.

The first problem solved is finding the deposit value for a uniform series using A/F.

The second method uses the equation, A =$100,000*(A/F,7%,8)=$9746.71. The value is the same as estimated by the cash flow moment method.

A/F can be estimated by using the formula, A/F=(i)/((1+i)^n-1), i=7%,n=8. We substitute to get A/F as (0.07)/((1.07)^8-1))=0.09746. The value will be multiplied by $100,000 to get the A value. A value will be $100,000*0.09746=$9746.78.

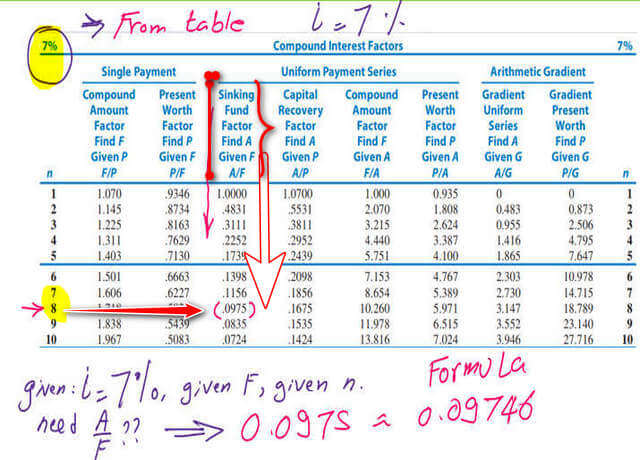
A table was used to find the deposit value for the uniform series, which was i=7%.

The next method uses the interest rate table. We use the 7% interest rate table; we have an n value equal to 8. We need to find the A/F value. Check the sinking fund factor A/F to find A in terms of F. We go vertically and find the intersection with n=8; we get the value of 0.0975. This number matches the previous calculations.

Use the Excel function PMT to find the deposit value for the uniform series.

Another way to get the value of A/F is by using the Excel function P.M.T. The P.M.T. (rates, which are 0.07, Nper is eight deposits, PV stands for present value,0, Fv stands for the future value, which is $100,000, and type is zero). The A value is by a minus sign since uniform series are outflows.

If we use an Excel sheet, use cells. Cell C19 has an interest rate of 7%. The N periods are 8. Cell C21 is for a

Future value F is equal to 100,000. In the last cell, C23, we can get the A value as a minus. I have taken a screenshot of the cell.

PMT(C19,C20,0,+C21). The A value can be obtained by using the Excel sheet.

A second solved problem is finding the A for a uniform series: use the cash flow moment.

Check another problem, 2.12, paying off an education Load: Find A, Given P,I, and N. This is another way to get A, but this time in terms of P, where P is the present value. You borrow from the bank to finance your educational expenses. The loan should be returned to the bank during the next five years.

The rate of interest is 6% yearly. The payment should be in equal annual installments. The loan will be paid off over five years. As we know, for the uniform series, paying is done starting one year after getting the loan.

The first installment is due a year later. Estimating the amount of the annual installment A is required. Refer to Figure 2.20. This solved problem requires estimating A in terms of P, while the previously solved problem requires estimating A in terms of F.

In this solved problem, I and n are given. First, we will use the method of estimating the moment of cash flow about the pivot point. Take the pivot point at time t=0. If P is pointing upwards, then it is +P.

The moment arm for P is (1+i)^0, whether from right or left, the P coincides with the point, and the arm length is equal to 1.

. The sum of moments is equal to zero. P will be as L.H.S, and the product of A by the arm will be set as R.H.S with a changing sign.
The negative exponents are considered fractions.

The equation is modified as we can see , P=A*(1/(1.06)+1/1.06^2)+1/(1.06)^3++1/(1.06)^4+1/(1.06)^5)). The P-value is $21061.82. we equate to the correct value (4.2123)*A. Finally, the A value is $5000.

This is another alternative, using the pivot point at time t=1. The sum of moments is shown based on the selected pivot point. Please refer to the right side of the slide picture for a comparison between cash flow moments based on a pivot point at t=0 and at a pivot point at t=1. Finally, the A value is $5000.

Use the expression of A/P to find the deposit value A for uniform series.

We use an equation where A=P(A/P, i,n), P is given, and A is unknown. P=$21061.82. A/P value can be obtained from the known equation as equal to (i*(1+i)^n/(1+i)^n-1)). The A/P value is equal to 0.2374. A/P will be multiplied by P. The deposit value A =21061*0.2374=$5000. The same value for A matches with the previous calculation by the moment of cash flows.