Last Updated on October 26, 2024 by Maged kamel

Steel columns and Euler’s formula-part 2.

In this post, Steel Columns and Euler’s formula-part 2, we will discuss the different shapes of steel columns & how to derive Euler’s formula, and lately, the modes of failure for columns.

Structural steel shapes and their use for steel columns.

The first shape is the single angle. The second shape in b is a double angle back to back, in T section and w columns, etc, and the round shape. He started talking about each element and where it should be used, for instance, a single-angle member section used as bracing and compression in a light truss. Equal angles are more economical than unequal angles because their least r values are greater for the same area of steel.
     

The double angles are likely to be used in trusses as a top chord, which might consist of a pair of angles back to back for section b.

The angles are spaced to insert the guest plate so they will be back to back. An examination of this section will show that using unequal leg angles with long legs is probably desirable back to back.

If you wish to have extra lateral support, use the C channel. W sections are suitable for use as columns for buildings and compression members in a highway bridge. The radius of gyration values are different.

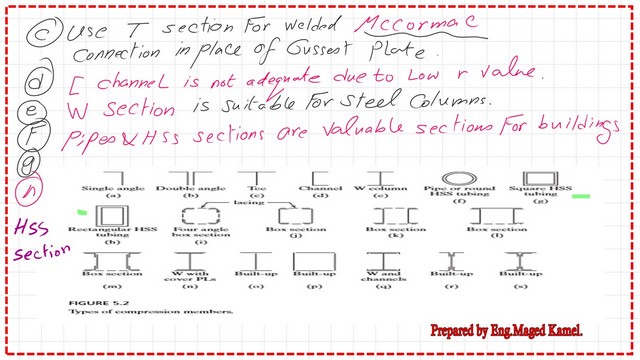
The next slide image shows more details about box sections.

Types of modes of failure.

Compression members can fail in three general modes of failure:
1-Flexural buckling, or Euler’s buckling, the members will buckle about the least radius of gyration for the section.

2-  Local buckling: some parts of the cross-section will buckle locally in compression due to slender compression members.   
 3-Flextural Torsional buckling for members that have a certain cross-section configuration.

Derivation of Euler’s formula.

We are all familiar with the double integration method.    Euler’s formula depends on estimating the moment caused by a compression force  P*y= E*Iy”, where y” is the curvature.                                                                       
     1-Multiply by 2*dy, Integrate one time to get the expression for the deflection since this equation is in the general form.

2- then from the boundary condition, establish a value for C1 by considering- dy/dx=0 at L=L/2.

3- After several mathematical operations, we get the value for The critical load Pcr that the column can carry.

The critical buckling load

P =π^2 EI/L^2, where Pcr is the critical buckling load, which is the max load that the column can carry, and the stress For can be estimated by dividing the critical load /area and recall that the Inertia I can be expressed as the multiplication of A*r^2.

The stress can be evaluated as Fe=π^2 EI/(L/r)^2, which can be written as Fe while getting this expression as assumed that the curve starting from zero at end support and increasing to the delta, at the middle and then he got that expression.

But in reality, several different end conditions exist, which is why the k expression is introduced in the expression. As a result, the L can be rewritten as ( k L). The equation of Fe will be set =π^2 E/(KL/r) 2, where KL/r is called the slenderness ratio, and K is the effective length factor that modifies the actual column length and supports conditions.

The following slide image gives a better understanding of the failure modes of compression columns. Two columns are shown; the first has a general or elastic buckling. The second column has a local buckling due to the fact that the ratio between width and thickness is small,

The modes of failure for short columns. 

There are two modes of failure: ductile failure will have a short, bulging shape, while brittle failure will have a shear failure with a slanted angle.  

The next slide shows the different modes of failure for columns based on

For the next post-2-Buckling for columns – effective length factors.
For an external resource-chapter 7– Concentrically Loaded Compression Members