Last Updated on March 1, 2026 by Maged kamel
Euler’s formula-part 2.
In this post, Steel Columns and Euler’s formula-part 2, we will discuss the different shapes of steel columns & how to derive Euler’s formula, and later, the modes of failure for columns.
Structural steel shapes and their use for steel columns.
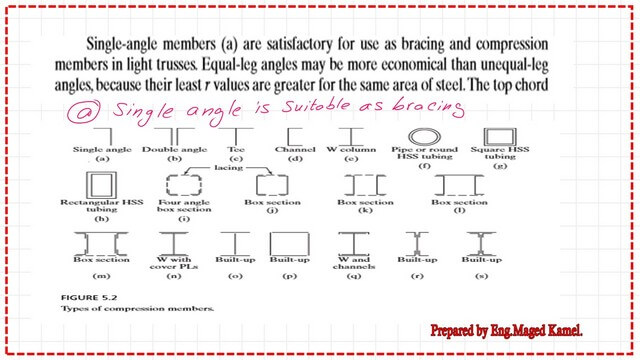
The first shape is the single angle. The second shape in B is a double-angle, back-to-back, in T-sections and W-columns, etc., and the round shape. He began discussing each element and its appropriate applications, for instance, a single-angle member section used as bracing and compression in a light truss. Equal angles are more economical than unequal angles because their least r values are greater for the same area of steel.
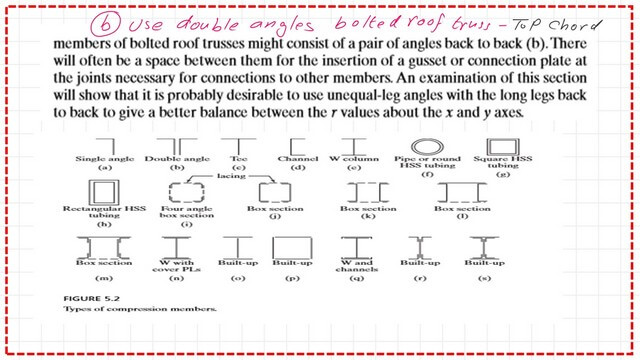
The double angles are likely to be used in trusses as a top chord, which might consist of a pair of angles back to back for section B.
The angles are spaced to insert the guest plate so that the guest plate is back-to-back. An examination of this section will show that using unequal leg angles with long legs is probably desirable back-to-back.
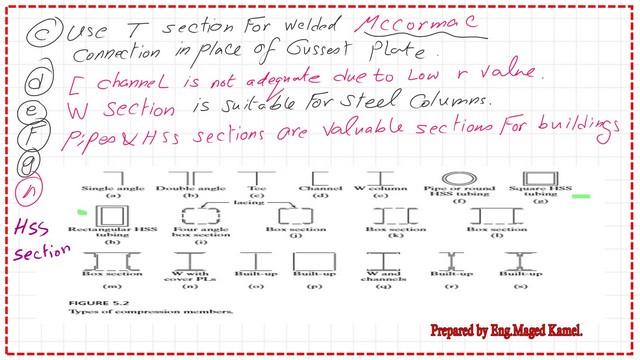
If you wish to have extra lateral support, use the C channel. W sections are suitable for use as columns in buildings and as compression members in highway bridges. The radius of gyration values are different.
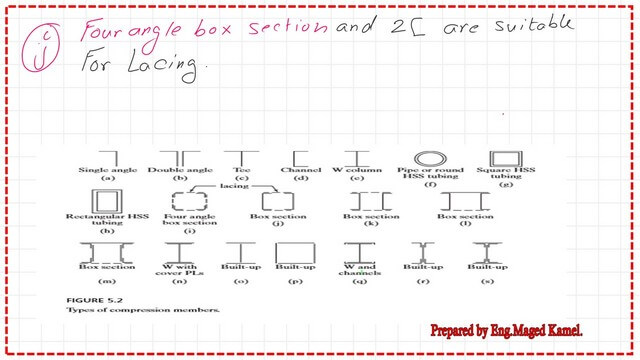
The next slide image shows more details about box sections.
Types of modes of failure.
Compression members can fail in three general modes of failure:
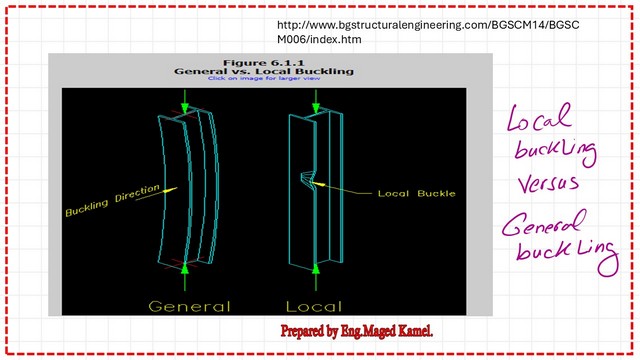
1-Flexural buckling, or Euler’s buckling, occurs when the members buckle about the least radius of gyration for the section.
2- Local buckling: Some parts of the cross-section will buckle locally in compression due to slender compression members.
3-Flextural Torsional buckling for members that have a particular cross-section configuration.
Derivation of Euler’s formula.
We are all familiar with the double integration method. Euler’s formula depends on estimating the moment caused by a compression force P*y= (E*Iy”), where y” is the curvature.
1-Multiply by 2*dy, integrate once to get the expression for the deflection, since this equation is in the general form.
2- then from the boundary condition, establish a value for C1 by considering- dy/dx=0 at L=L/2.
3—After several mathematical operations, we get the value for the critical load Pcr that the column can carry. The critical load depends on E, the modulus of elasticity for steel, 29000 ksi, I, the inertia value of the section, and the effective length of the column.
The critical buckling load
P =π^2 EI/L^2, where Pcr is the critical buckling load, which is the maximum load that the column can carry, and the stress For can be estimated by dividing the critical load /area, and recall that the Inertia I can be expressed as the multiplication of A*r^2.
The stress can be evaluated as Euler’s stress, Fe = π^2 EI/(L/r)^2, which can be written as Fe. This assumes that the curve starts at zero at the end support, increases to the delta at the middle, then follows that expression.
But in reality, several different end conditions exist, which is why the k expression is introduced in the expression. As a result, the L can be rewritten as (kL).
The equation of Euler’s critical stress Fe will be set =π^2 E/(KL/r) 2, where KL/r is called the slenderness ratio, and K is the effective length factor that modifies the actual column length and supports conditions.
The following slide image gives a better understanding of the failure modes of compression columns. Two columns are shown; the first has a general or elastic buckling. The second column exhibits local buckling because the width-to-thickness ratio is small.
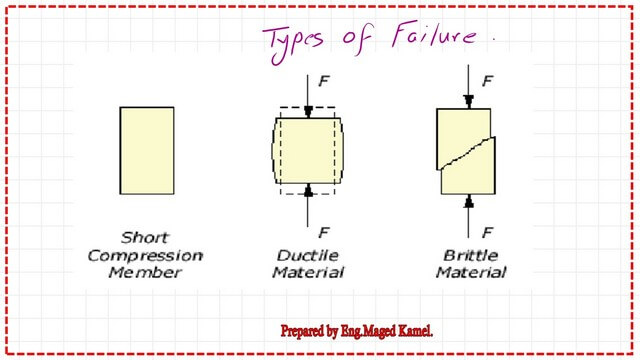
The modes of failure for short columns.
There are two modes of failure: ductile failure will have a short, bulging shape, while brittle failure will have a shear failure with a slanted angle.
The next slide shows the different modes of failure for columns, based on flexural and Torsional buckling.
The PDF for this post and the previous post can be viewed or downloaded from the following link.
For the next post-2- Buckling for columns – effective length factors.
For a good A Beginner’s Guide to the Steel Construction Manual, 14th ed. Chapter 7 – Concentrically Loaded Compression Members.
For a good A Beginner’s Guide to the Steel Construction Manual, 15th ed. Chapter 7 – Concentrically Loaded Compression Members.
For a good A Beginner’s Guide to the Steel Construction Manual, 16th ed. Chapter 7 – Concentrically Loaded Compression Members